If we claim the Internet as the greatest invention of the 20th century, which has revolutionized how we communicate every day and turned our lives upside down, today’s stage certainly belongs to quantum Internet, which would deeply change our way of thinking as well. Quantum networks lay the cornerstone of quantum communication and quantum computation systems. Similar to classical networks, it allows for the transmission of quantum information between physically separated quantum processors. An enabling technology for future quantum networks is that of quantum repeaters (QRs).
What is quantum repeater
The direct distribution of quantum states is limited by transmission losses of the channel (usually the optical fiber or free-space, the same as classical world) used. Even under certain optimistic assumptions for the technology evolution, the achievable distances are limited to a few hundred kilometers. Unlike in classical world, where amplifiers can be deployed to boost or regenerate the signals, here, this idea fails due to the fact that quantum states cannot be copied or “amplified” without any disturbance, known as the no-cloning theorem.
QRs were initially proposed to enable quantum information distribution at long distances, relying on the pillar of the quantum palace—entanglement. Using teleportation techniques, one can then send quantum information across the network once some entanglement is shared between users. The main idea behind it is to first distribute and store entanglement between short segments and then to use entanglement swapping (ES) and entanglement distillation (ED) at intermediate stations to establish entanglement over long distances.

The pioneering works
Theoretically speaking, QRs have gone through a number of development stages. Based on how ES and ED operations are performed, most of them fall into two categories: the probabilistic ones and the deterministic ones. The probabilistic QRs use photonic systems for both distribution and swapping of entanglement. Due to its inherent fragility against loss, after each operation, we have to wait for either good news so that we can move on to the next step or bad news that we have to repeat another trial until succeed, both of which rely on two-way classical communication. You can imagine how this back-and-forth will result in a long coherence time and a low generation rate. However, despite those disadvantages, probabilistic QRs are perhaps the simplest setups that can be implemented in practice. The pioneering work of this type is developed by Duan, Lukin, Cirac and Zoller in 2001, known as DLCZ, where they used atomic ensembles and linear optics to achieve the goal.
Actually, when the concept of QRs was originally introduced by Briegel, Dür, Cirac and Zoller (BDCZ) in 1998, ES and ED operations were designed in a deterministic, but possibly erroneous gate-based way, where they proposed a nested purification protocol to permit efficient quantum communication over distances longer than the attenuation length. However, their model is still based on two-way classical communication for the confirmation of each attempt, which, in effect, turns a deterministic setup to a probabilistic one, suffering similar drawbacks mentioned above.
Quantum repeaters with encoding
The most recent QR proposals totally eliminate the necessities of two-way classical signaling and only use quantum error correction (QEC) to copy with loss and operational errors. They enable us to directly send quantum states across a communication channel hop-by-hop. The key idea resembles the one used in classical communications network, in which message bits are encoded with some redundancy such that at the receiver the original message can be retrieved. Such structures offer an improvement in quantum data rate at the price of requiring much more demanding quantum computational capabilities, which will be further away in terms of an experimental demonstration.

What I am working on
In the spirit of having an eye on near-future implementations, my focus is on the transition from probabilistic QRs to deterministic QRs that use quantum error correction techniques only for their ED operations, while entanglement over short links is still established in a probabilistic and heralding way. In such QRs, using a number of bipartite entangled states (yellow lines in Fig. 3(a)), we create a multi-qubit entangled codeword across elementary links (yellow shade in Fig. 3(b)). As we apply the ES operations, this codeword structure will then allow us to correct some of the errors that happen because of imperfections in the employed gates, measurement modules, and/or the initially distributed bipartite states.
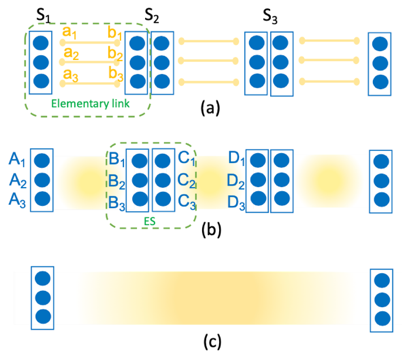
In principle, one can choose different code structures to implement such systems. Here, we use the repetition codes to study and develop our methodology. They offer a simple structure, which can make their implementation easier, and still have relevance in systems where one type of error is more dominant than the other. We develop reliable tools which relies on the linearity of the quantum circuits and the transversality of the code employed to manage the complexity of the analysis. Previous work on this subject often relies on various approximations to analyze the system. Here, we try to remain as close as we can to the exact results and only use approximations that are analytically justified and numerically verified. This accurate approach shows that such systems are more resilient to errors than previously thought, which can make their near-future implementation more viable.
Using our methodology, we study the performance of QKD systems run over QRs with three- and five-qubit repetition codes by accounting for various sources of error in the setup. We fully study the effect of different terms, components, and system imperfections on the secret key generation rate of the QKD system, and how one can use the information obtained during entanglement swapping and decoding stages to maximize the rate. We show that, so long as QKD is concerned, error detection features of the code may be even more relevant than its error correction functionalities. We find that the majority of secret key bits come from the portion of the data that corresponds to no detected errors in either the repeater chain or decoder modules (we call it the golden state in Fig. 4).
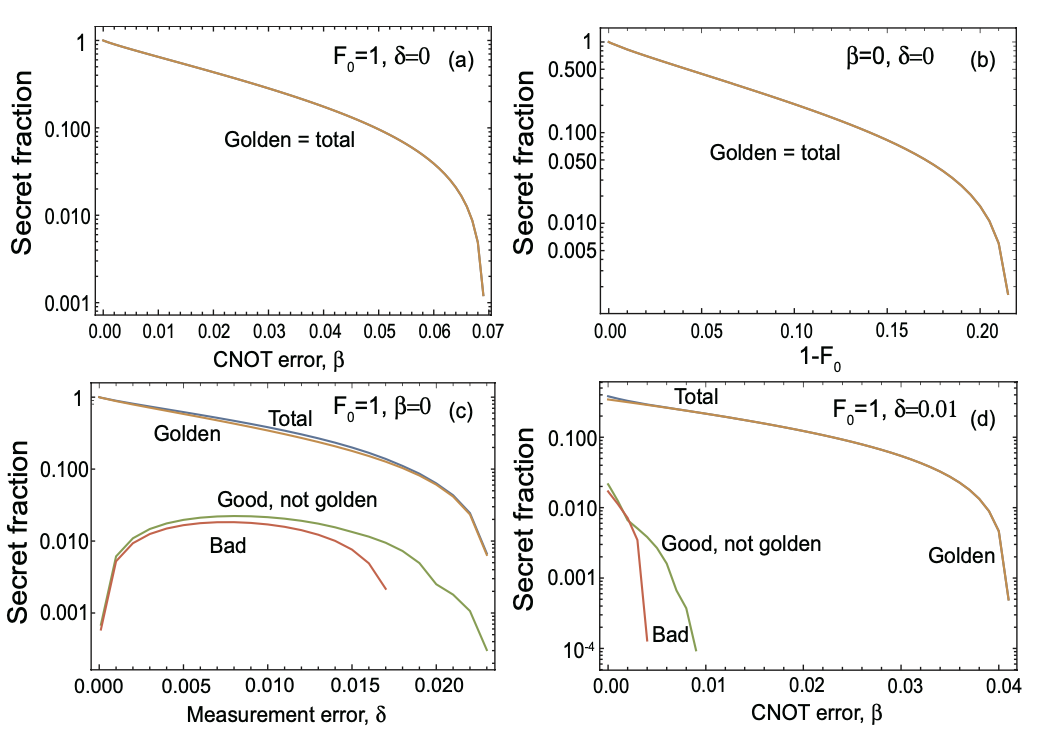
We further expand our study by proposing two alternative decoder structures that only rely on single-qubit measurements, which not only simplifies the implementation aspects but also, by removing the major source of error from decoding circuits, results in better performance in many practical scenarios. We benchmark the performance of the QKD system that runs on this type of QRs with probabilistic QRs which do not necessarily use any additional distillation techniques, and quantify the regimes of operation, where one class of repeater outperforms the other. We find that for most practical purposes, the simple three-qubit system is our best choice.
Our analysis suggests that extending the reach of trust-free terrestrial QKD links to 1000km is within reach in the near future. If you would like to know more details, click here!