Introduction
Quantum Key Distribution (QKD) enables secure key agreement with information-theoretic security. This is in contrast with classical key agreement protocols whose security is based on computational hardness conjectures. Hence, QKD can offer a distinctive security advantage over classical techniques, particularly in contexts where long-term security is sought.
Current QKD systems have now reached performance levels essentially comparable to the fundamental limits on the secret capacity. This indicates the impressive technological maturity that quantum communications engineering has reached. Conversely, this also fundamentally limits our hope to experience large performance gains for QKD in the future. Extending the functionality and overcoming the performance limitation under which QKD can operate requires either quantum repeaters or new security models.
We address this issue in an alternative way by investigating the latter option. Our approach consists of devising a new security model that leverages short-term computational security and noisy quantum storage to boost the performance and functionality of quantum-based key agreement. Interestingly, although our proposed model is weaker than the unconditional security, it provides everlasting security, i.e., security of key establishment against a computationally unbounded adversary, provided an initial ephemeral encrypted communication cannot be broken within a short time. As everlasting security is not achievable using computational constructions, our hybrid approach can claim a strict security gain compared to classical techniques, in addition to significantly extending the performance envelope.
Timelock
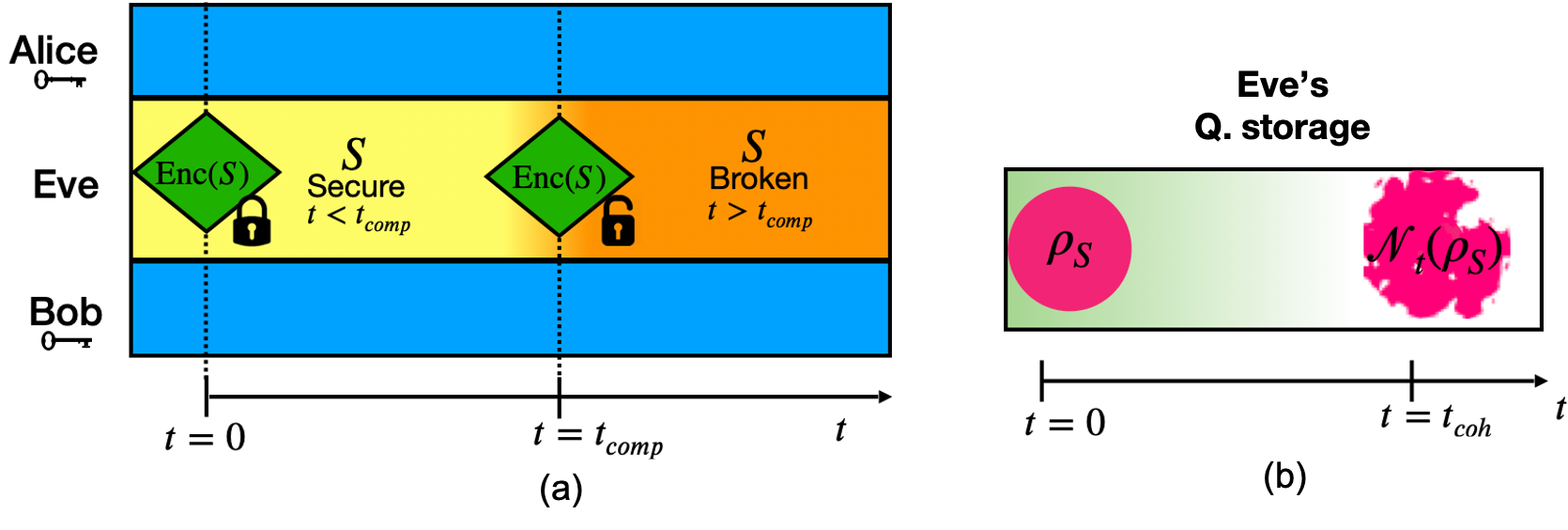
A timelock is a part of a locking mechanism commonly found in bank vaults and other high-security containers, designed to prevent the opening of the safe or vault until it reaches the preset time. An authorized employee of the bank can open the vault. However, any unauthorized thief or attacker trying to break into the vault cannot open it before this preset time. Combined with an extra security mechanism, such as an alarm alerting the Sheriff, the time-lock forms a very effective security mechanism. Quantum Computational Time-lock construction will essentially follow the same principle; however, in that case, a computational one-way function will play the role of the time-lock mechanism, while the decoherence (of quantum storage) plays the role of the Sheriff.
Quantum Computational Timelock security model
We introduce a novel security model, the Quantum Computational Timelock (QCT) security model, which consists of two nested assumptions:
- Alice and Bob are assumed to have access to an encryption scheme, computationally secure for a short time, to do private communication against Eve.
- Eve’s quantum memory is decohering over time such that computationally secure encryption may only be broken after time much longer than the coherence time of available quantum memories.
These assumptions, in particular, are well motivated by reality, as the coherence time of a state-of-the-art quantum memory, O(1) sec, is much smaller than the computational time, ~30 years, for which a current classical cryptographic scheme is secure.
MUB-QCT Key distribution in the QCT security model
We present a novel key distribution protocol in the QCT security model. We call it the MUB-QCT protocol, where two essential ingredients used are a complete set of mutually unbiased bases (MUB) and a full set of pair-wise independent permutation.
Alice and Bob, who have access to short-term secure computational encryption, use it to exchange the basis information (a MUB and a permutation, chosen randomly) over a classical channel. The key bit is encoded onto a quantum state of a d-dimensional Hilbert space using this basis. The quantum state is then sent over a quantum channel by Alice, received, and decoded by Bob by measuring on the exchanged basis. After n channel uses the raw keys are exchanged, and finally, Alice and Bob perform classical post-processing on their exchanged raw keys and transform them into a pair of secret keys.
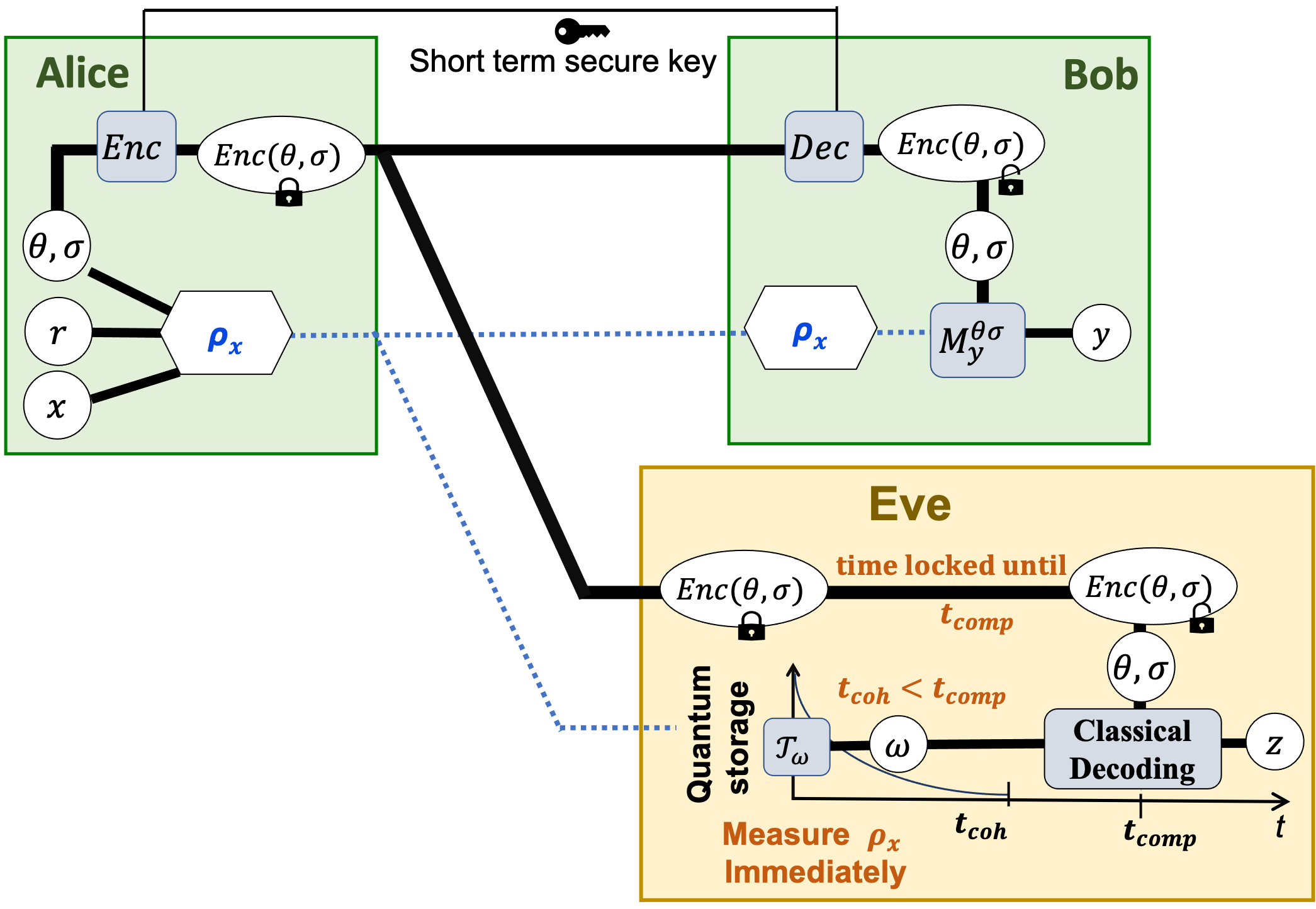
The optimal attack strategy for non-authorized party Eve consists of an immediate measurement followed by classical post-processing on measurement data. This strategy is known as state discrimination with post-measurement information as described. Moreover, this optimal eavesdropping strategy reduces accessing the output of a strong Quantum to Classical randomness extractor (QC-Extractor) based on a full set of MUBS.
The main requirement to prove the security of the MUB-QCT protocol is to bound Eve’s mutual information I(X; Z). Following the optimal eavesdropping, we can achieve this in the QCT security model by only considering the input state and establish I(X; Z) ~ O(1/d).
Performance Analysis
High dimensional encoding in the MUB-QCT protocol allows high resilience to noise by offering a maximum tolerable error rate of up to 50% for large d.
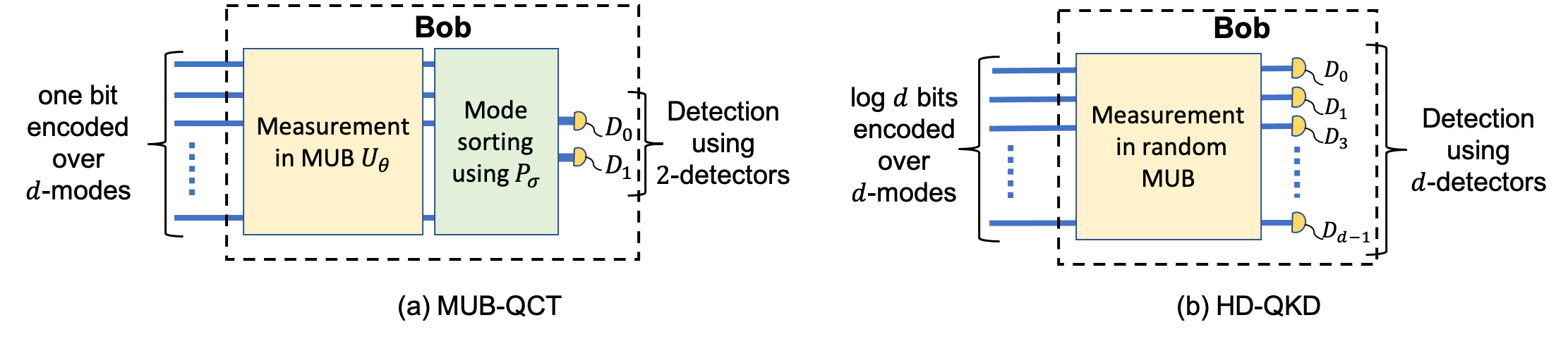
The MUB-QCT protocol’s detectors requirement remains fixed, i.e., two detectors (to distinguish a bit), irrespective of d. This significantly relaxes resource requirements compared to HD-QKD schemes, which require d-single-photon detectors.
In the MUB-QCT protocol, Eve’s information can be upper bounded only by considering the state that Alice inputs. Consequently, the implementation of Bob’s measurement device is not required to be trusted to guarantee security.
MUB-QCT with multiple quantum state copies
We also explore if the MUB-QCT protocol offers high tolerance to the channel loss incurred at long-distance by transmitting multiple photons per channel use. We prove that under a restricted scenario, where Eve proactively measures each copy in a different MUB followed by post-measurement classical decoding, the MUB-QCT protocol allows performing secure key distribution with input states containing up to O(d) photons. Implying, a significant performance increase, characterized by an O(d)-multiplication of key rates.
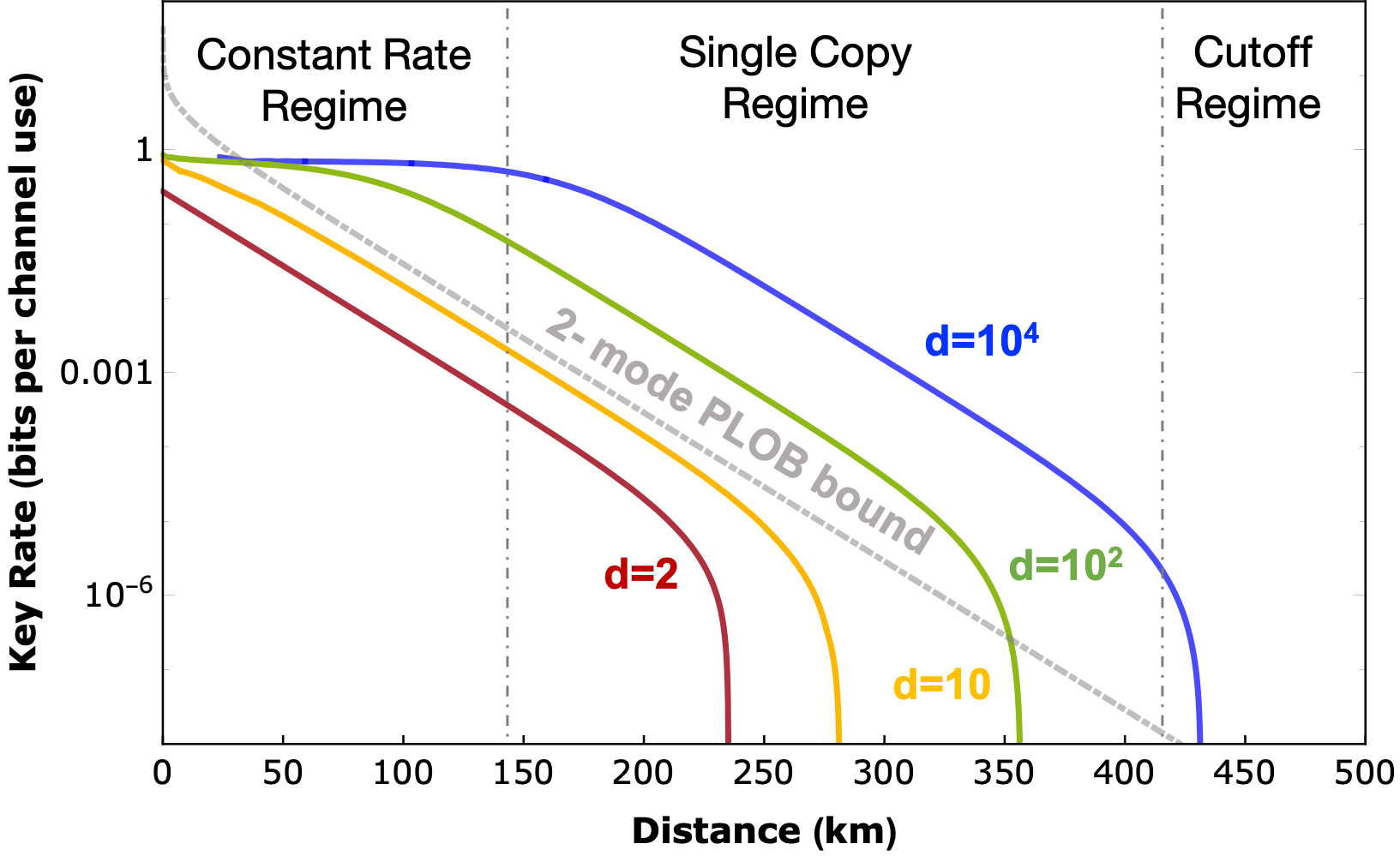
Moreover, the possibility of sending multiple copies of the quantum state per channel use can be averaged to realize multiparty key distribution. In principle, Alice can transmit m copies to up to m authorized Bobs, allowing them to distill the same key.
However, the security analysis presented so far does not account for general attacks (collective measurements and adaptive strategies). We do not know if the proactive MUB measurement is optimal. Thus, the question of the optimal attack in the multiple copy case remains open and a direction for our future work.
Conclusion
We proposed a new Quantum Computational Timelock (QCT) security model. We assume that an encryption scheme is computationally secure for a short time, much longer than the coherence time of available quantum memories. The notion of short-term secure encryption is similar to the notion of time-release encryption (TRE). In contrast, the notion of time-limited quantum memory is similar to quantum storage in the noisy storage model.
We constructed the MUB-QCT key distribution protocol using a complete set of Mutually Unbiased Bases (MUBs). We prove the security by upper bounding Eve’s information as I(X; Z)~ O(1/d) for the optimal eavesdropping attack strategy, which reduces access to the output of a strong QC-extractor. Moreover, Alice can send O(d) copies per channel use when Eve is restrictive to perform proactive MUB measurements. As a result, the protocol offers high resilience to error (up to 50% for large d) with fixed hardware requirements, measurement device-independent (MDI) security which relaxes some significant engineering constraints concerning quantum key distribution (QKD), and O(d) multiplication of key rates.
Our work is particularly related to Quantum data locking, where the security against an adversary with time-limited quantum memory can be proved by upper bounding the accessible information. However, existing work on quantum data locking is restricted to single-photon encoding. It cannot extend the distance or resort to constructions based on random coding arguments for which practical implementation with structured measurement is not possible.
Hence, our results illustrate that hybrid approaches to quantum cryptography might constitute a practical and promising route to extend the performance and functionality of quantum cryptography while still guaranteeing everlasting security, which is not achievable through classical means.