Federico works on theoretical progress in multi-party quantum key distribution, also known as quantum conferencing. Have you ever heard about it?
Your data is under threat
In recent times people, as well as institutions, companies and governments, are increasingly concerned about the privacy of their data and are constantly looking for better ways to keep it safe.
One of the instances in which private data becomes vulnerable is when it is transmitted from one party to another one (e.g. a bank and its customer, the secret services and the government, etc.). In order to keep the data safe, the sender encrypts the data with a secret key -the encryption key- that he/she shares with the receiver, prior to transferring it. The receiver then decrypts the data using the same secret key. A potential eavesdropper cannot learn the data without the encryption key. Hence, the data is secure as far as the key shared by the sender and the receiver through a cryptographic scheme is secret.
Classical Cryptography
Nowadays, the standard cryptographic schemes in use are referred to by quantum physicists in my field as “classical cryptography“. The security of such schemes relies on assumptions on the adversary’s computational capabilities , thus being vulnerable to retroactive attacks. In other words, an adversary could intercept and store the data encrypted by a classical crypto scheme, waiting to have sufficient computational power to decipher it. The recent developments of quantum computers, which promise unprecedented computational power, further increase the vulnerability of classical cryptography.
Quantum key distribution is the cure
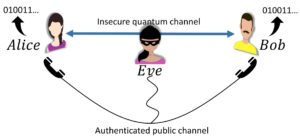
Quantum theory, despite being a threat to current cryptographic schemes, also provides a solution. Indeed, the mentioned security concerns and the prospect of commercialization boosted major advancements in the field of quantum cryptography and particularly in quantum key distribution (QKD).
A QKD protocol enables two parties, Alice and Bob, to generate a shared secret key by sending quantum systems (typically photons of light) through a quantum channel that can be under the control of the eavesdropper (Eve), and by measuring the systems upon reception. Alice and Bob are also equipped with an authenticated public channel, e.g. a phone call wiretapped by Eve.
By relying on intrinsic properties of quantum theory, QKD can be unconditionally secure regardless of the eavesdropper’s computational capabilities, unlike classical cryptography. This remarkable feature of QKD allows for ever-lasting secure communication and attracted the attention of companies, private institutions and governments.
QKD has been successfully implemented over 400 km of optical fibers and over 1000 km of satellite-to-ground links, and has already reached the market with companies like Toshiba and ID Quantique.
What makes QKD secure?
The unconditional security offered by QKD is based on distinctive quantum features, such as entanglement. When two or more quantum systems are entangled, their properties are strongly interconnected. Indeed, measuring a property on one quantum system immediately determines the measurement outcome of the same property on the other systems. This fact can be used to generate correlated outcomes when different parties perform the same measurement on their entangled quantum systems. The correlated outcomes can then be used as a shared key.
The key generated in this way is secret thanks to the monogamy of entanglement. According to this peculiar feature of entanglement, if two parties are strongly entangled, a third party shares little entanglement with them. The entangled parties can thus obtain a shared key with their highly correlated measurement outcomes while being sure that the third party -a potential eavesdropper- has little information about it.
Quantum conferencing
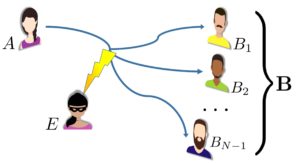
The task of QKD can be generalized to more than two parties through a conference key agreement (CKA), where the goal is the establishment of a shared secret key -a conference key– among several parties. The conference key can then be used by one party to securely broadcast a message to the remaining parties.
The CKA could be trivially realized by performing bipartite QKD schemes between pairs of parties and using the established keys to distribute the conference key. Alternatively, one can exploit the correlations arising in multi-partite entangled states and devise a CKA protocol which directly outputs a secret conference key. Such truly multi-partite schemes are a natural application of quantum networks and have been proven to be advantageous in certain network configurations and noise regimes. In this post we focus on the latter type of CKA (the first review on this research topic [“Quantum Conference Key Agreement: A Review”, Murta, Grasselli, Kampermann and Bruss, 2020] is going to be published shortly).
The multiparty BB84 protocol
The BB84 protocol, devised by Bennett and Brassard in 1984, is the first and arguably the most famous of all the QKD protocols. Due to its simplicity, variants of the protocol have been widely implemented and even commercialized.
In our first work in the QCALL network, we generalized the BB84 protocol to a scenario with an arbitrary number of parties “N” willing to share a conference key, obtaining the so called N-BB84 protocol. Based on our work, an upcoming experimental implementation of a four-party BB84 protocol is about to be published [Proietti, Ho, Grasselli, Barrow, Malik, Fedrizzi, 2020].
The security proof of most QKD protocols is initially performed in a simplistic scenario, i.e. when the parties exchange an infinite number of quantum signals (asymptotic scenario). This is, of course, far from reality but it greatly simplifies the proof and gives indication on the protocol’s real-life performance.
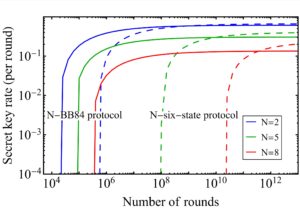
A more realistic security proof with a finite number of signals (finite-key scenario), must consider that the measured data in the execution of the protocol is affected by statistical fluctuations. The challenge is to guarantee unconditional security of the distilled secret key despite the statistical fluctuations affecting the data.
In our work, we proved the security of the N-BB84 protocol and of another existing multiparty protocol (the N-six-state protocol) in the finite-key scenario, when the eavesdropper is allowed to perform the most general attack on the quantum channels (coherent attack). We also compared the performances of the two protocols under realistic conditions and showed that the N-BB84 protocol requires a lower number of protocol rounds to produce a non-null secret key.
Achieving longer distances
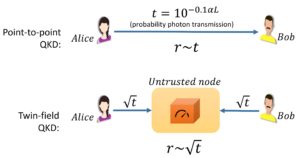
Most of the early QKD protocols do not rely on any intermediate relay: the parties taking part to the protocol are connected by a single-piece quantum channel. Such protocols are often called point-to-point schemes.
In spite of the great distances experimentally achieved by point-to-point QKD protocols (see above), their key rates are fundamentally limited. The key rate “r” of a QKD protocol is given by the number of secret key bits per protocol round (in a round one or more parties send a quantum signal) and its value is typically well below 1. Clearly, in any point-to-point QKD scheme the key rate cannot exceed the probability “t” that the signal sent by Alice reaches Bob.
The problem is that most QKD protocols employ photons as information carriers and the probability “t”of a photon traveling the distance “L” separating Alice from Bob decreases exponentially with “L” ! (see figure) Thus, key rates of point-to-point QKD schemes decrease exponentially with the distance, strongly constraining their long-distance applicability.
A solution to this limitation is provided by the recently-developed twin-field (TF) QKD protocol, initially introduced by our QCALL partners in Toshiba. In TF QKD, Alice and Bob prepare weak coherent pulses corresponding to a random bit they picked and send them to a central untrusted relay. The relay combines the pulses, measures them, and announces the measurement outcome. Based on the outcome, Bob either flips his bit or does nothing, in order to match it with Alice’s. By repeating this procedure at every round, the parties establish a secret key, which cannot be retrieved by the untrusted relay, even with the information of the measurement outcomes.
Being TF-QKD based on single-photon interference events occurring in the untrusted node, only one photon out of the two sent by Alice and Bob needs to arrive at the central relay at every round. Thus, the key rate of TF-QKD scales with the probability that one photon covered half of the total channel length (square root of “t”). This implies a square-root improvement in the performance over point-to-point QKD protocols, allowing to reach longer distances.
TF-QKD is currently the only experimentally implemented protocol with an improved scaling of the key rate versus the distance, making it the new benchmark for far-distance QKD.
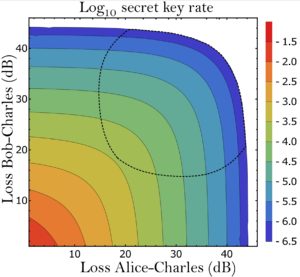
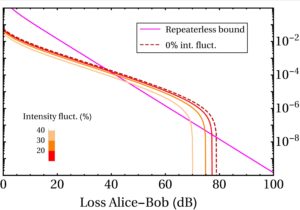
With a first and a second publication in collaboration with our QCALL colleagues in Vigo, we investigated the practical performance of the TF QKD protocol proposed by Curty et al. In particular, we optimized its key rate when the distances separating Alice and Bob from the untrusted node differ and showed that the protocol can achieve good key rates even in extremely asymmetric scenarios. We also showed that the protocol is robust against intensity fluctuations affecting the parties’ lasers (figures above).
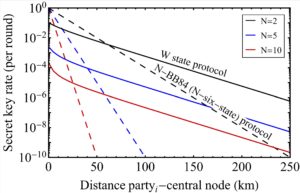
Inspired by the TF-QKD protocol, we extended its founding idea to the multiparty scenario. We introduced a CKA where N parties simultaneously establish a conference key by relying again on single-photon interference. The protocol, also called “W state protocol”, presents a remarkable improvement in the key rate-vs-distance compared to its point-to-point couterpart, just like TF-QKD (see figure).
Indeed, in the W state protocol just one photon out of the N photons sent by every party needs to arrive at the central relay, while in point-to-point multiparty protocols like the N-BB84 (and N-six-state), each of the N photons must be successfully transmitted. We proved the security of the W state protocol in the finite-key regime and for general attacks.
For the security paranoids
QKD offers an exceptional level of security, provided that the assumptions on the devices used for its implementation are experimentally verified. However, the devices could be affected by imperfections difficult to characterize, or, much worse, they could be forged by the eavesdropper in order to learn the secret key. Therefore, it is challenging to ensure that the assumptions on the implementation of a QKD protocol are met in practice.

Fortunately, device-independent (DI) QKD can guarantee the same level of security independently of the actual functioning of the employed devices. In this framework, the devices used by the parties are modeled as black boxes (i.e. completely uncharacterized) producing an output upon receiving an input from the party. The parties collect a series of outputs (with correspondent inputs) by repeating the same procedure for several rounds, making sure that they are distant enough so that no signal can travel from their device to the other’s device. If the collected data cannot be explained by a local deterministic strategy (for which a third party in the middle instructs the devices on the output to produce), the parties conclude that their data exhibits non-local correlations. This means that it was produced by an entangled state shared by Alice and Bob’s devices. Thanks to the monogamy of entanglement, the secrecy of the parties’ correlated outcomes is restored, guaranteeing that the key distilled from the outputs is secret.
We are currently working on a project which aims at devising new and better-performing device-independent multiparty QKD protocols, in short: DICKA. The fundamental principle on which these protocols are based would be the same, just extended to more than two parties.
If you want to know how this will turn out, stay tuned!