Tag Archives: PLOB bound

Introduction

As we live in the era of internet, online shopping/banking, it is basically an everyday task to enter our passwords and credit card data on different websites. The encryption (so that a malicious third party cannot infer our actual data) of this sensitive data that we send throughout the internet is based on the fact that some mathematical problems are extremely difficult to tackle with our current computers. Specifically, it is practically impossible to factorize very large numbers. However, in the other direction, if a factor is known then it is really easy to determine its cofactor. This asymmetry in the difficulties can be converted into the most widely used public key cryptosystems, which is called RSA, after its inventors.

The natural (quite disturbing) question arises whether this kind of cryptosystem is going to stay secure in the future knowing how fast technology is advancing. It is even scarier if one considers the progress on the development of quantum computers. With quantum computers the task of factorizing large numbers becomes exponentially faster with the so-called Shor’s algorithm.

Solution: Quantum key distribution (QKD)

In 1984, with the appearance of the famous BB84 protocol, it became clear that quantum mechanics can be used to fight against the threat that comes with future quantum computers. With encoding information into quantum systems and performing quantum mesurements on them can in principle be used to create a secret key between two distant parties (usually called Alice and Bob). This method is called quantum key distibution (QKD), which can achieve an identical, random and secret bit string (consting of 0-s and 1-s) between Alice and Bob via the most fundamental laws of quantum physics thus security is no longer based on computational assumptions (opposed to RSA). This resource then can later be used to encrypt the messages with the so-called one-time-pad (OTP), that is, Alice adds the key to her message (also consisting of 0-s and 1-s) bitwise modulo 2 (which basically means that 1+1=0). Thus Bob can decrypt the encrypted message by adding the same key bitwise to the encrypted message.

The security is based on the no-cloning theorem, stating that it is impossible for an eavesdropper to make perfect copies of arbitrary quantum states. Note that for classical bits copying is possible, therefore this is an apparent advantage that quantum mechanics offers.

Some difficulties of QKD: Repeaterless bound and source imperfections

The idea of QKD is relatively simple and elegant but in order to be a mature technology that can be deployed world-wide for everyday use, it has to overcome some limitations. In my research I try to come up with solutions in order to improve the performance of different QKD protocols, or at least to identify their limitations. The performance of a QKD protocol is characterized by its secret key rate, that is the number of secret key bits a certain protocol can generate per transmitted signal.

Repeaterless bound

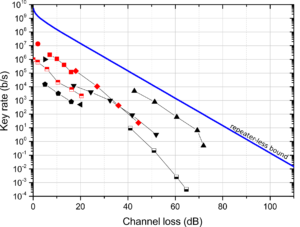
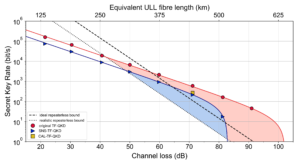
One important theoretical limitation on the performance of point-to-point (when the parties are directly connected via a quantum channel that can be for example an optical fiber, or even free space) QKD protocols is the so-called repeaterless bound. This bound for the achievable secret key rate is exponentially decreasing with the distance for long distances as it can be seen in Figure 1 (note the logarithmic scaling). This is caused by the fact that the probability that a photon survives travelling through the optical fiber connecting the parties decreases exponentially with the length of the fiber, this probability is called channel loss. As this is a very stringent limitation, it has to be overcome if long distances have to be covered by point-to-point QKD and one desires to have a reasonable secret key rate.

It is clear that intermediate nodes (repeater stations) between the parties have to be introduced to go beyond the repeaterless bound so that the photons do not have to cover the full distance between the parties (but only the half of it) to be useful for generating a secret key bit. If the channel loss corresponding to an optical fiber of length L is t then the channel loss for the half of the fiber is the square root of t.

The most recent solution to surpass the repeaterless bound is the so-called twin-field QKD (for more information see the spotlight article by ESR Mirko Pittaluga).

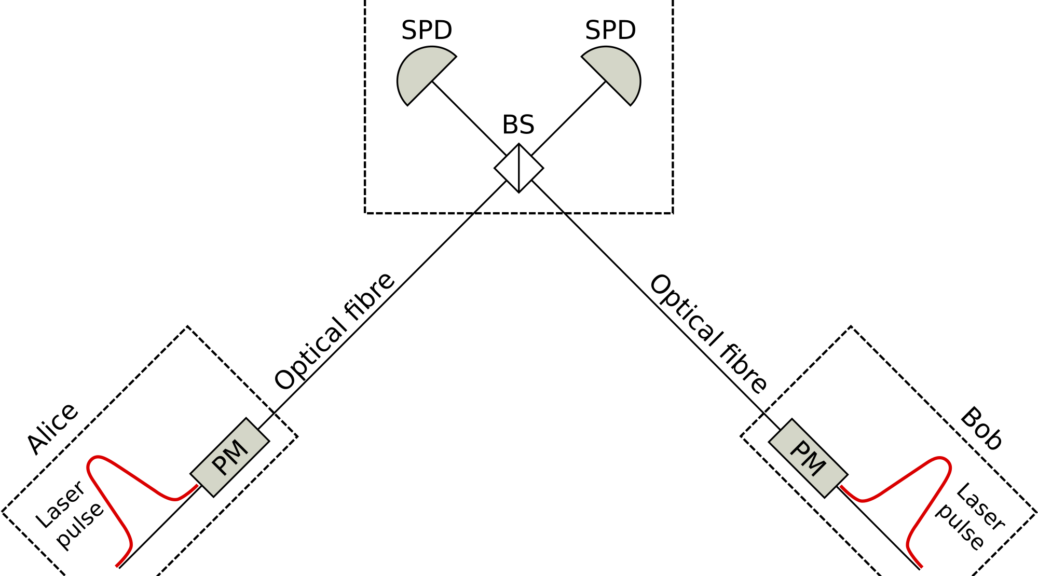
In my research, however, I focused on other types of approaches in order to overcome the repeaterless bound. The first one is a kind of adaptive QKD protocol, that is schematically depicted in Figure 2. The main point here is that the key generation process (denoted by BM in Figure 2) is only performed between successfully arriving photons (sccessful arrival is checked by the QND module), therefore, the key rate increases as every key generation trial is between actual signals that reached the middle station C. Otherwise it would be possible that a photon is lost on one side, which is not sufficient for establishing correlation between the parties.

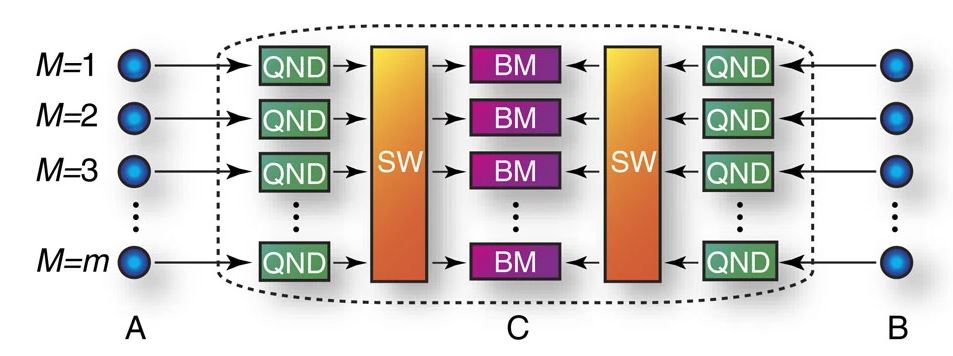
Figure 2. The schematic layout of the adaptive QKD protocol. Figure taken from !paper! — Figure 2. The schematic layout of the adaptive QKD protocol. Figure taken from this paper.

For the original proposal in Figure 2, idealized devices were assumed (e.g., perfect single-photon sources) and the authors showed that it is possible to overcome the repeaterless bound with this protocol.

In our work, we calculated the secret key rate of the original protocol if the idealized single-photon sources are substituted by the practical (and widely available) parametric down-conversion (PDC) sources (which sometimes emit two or more photons pairs). We found that with PDC sources the protocol is no longer capable of overcoming the repeaterless bound. Thus the performance is very sensitive to the imperfections of the devices.

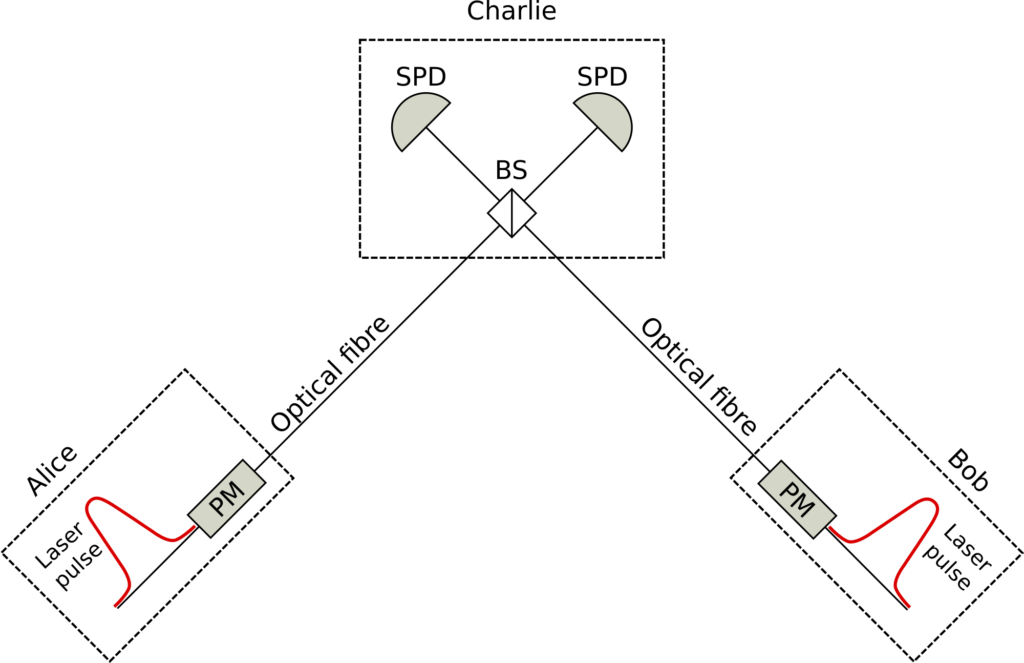
In, we investigated the performance of the protocol depicted in Figure 3, which is very similar to the protocol from Figure 2, but it is without QND modules and instead so-called quantum memories (QM) are applied in order to overcome the repeaterless bound. The QMs are able to store a quantum signal, therefore a quantum signal on one side can patiently wait until the signal from the other side successfully arrives and then a BM module carries out secret key generation. The working principle is the same as before, making sure that the key generation is only performed between actual signals.

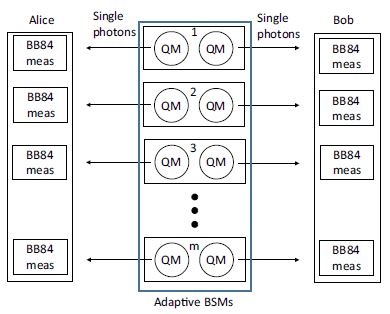
Figure 3. Schematic layout of the Quantum memory assisted protocol.

We characterized the necessary experimental parameters for the protocol to beat the repeaterless bound as a function of the applied QM pairs. The most important parameter of the devices is the dephasing time constant of the QMs, which describes how fast the stored quantum state changes over time (so higher quality memories have higher dephasing time constant as this depahsing leads to errors). We found that the requirement for the dephasing time constant of the QMs can be relaxed significantly if the number of QM pairs increases. But even with a lots of memory pairs it is far from trivial to overcome the repeaterless bound with current technology using this QM based protocol.

Source imperfections

The ideal information carriers for QKD protocols would be single-photons as a single-photon is a quantum mechanical object that cannot be copied due to the no-cloning theorem, however, in practice it is really challenging to implement on-demand perfect single-photon sources. Therefore, in the lab, the desired single-photon sources are approximated by dim laser pulses, but sometimes these pulses contain more than one photon. Whenever this happens, the information is not encoded only into a single entity but it is inherently duplicated so an eavesdropper Eve (who is only limited by the laws of quantum physics) can take one photon out of the two or more photons and keep it to herself thus she will have the same information carrier as Bob so the security of the protocol is compromised. This is called the infamous photon number splitting (PNS) attack. This means that additional techniques have to be applied to avoid the possibility of such an attack.

A simple protocol to fight against the PNS attack is the coherent-one-way (COW) protocol since it encodes the information coherently between different laser pulses and at the receiving end Bob checks that such coherence is kept. The PNS attack breaks this coherence, so the COW protocol should be able to detect it. Long distance experiments and even commercialized products have appeared based on this scheme. We show that, despite of its popularity, the COW scheme is not robust against other type of attacks.

Here, we designed an attack against the COW scheme, proving that all implementations of this protocol reported so far in the scientific literature are actually insecure. The attack is based on a technique called unambiguous state discrimination (USD). With USD it is possible to discriminate the different quantum signals (that Alice sends) without misidentifying them. This comes at the cost of sometimes obtaining an inconclusive result. If Eve applies this strategy in a clever way, she can remain undetected for the parties (she will not break the coherence between the signals) since she never makes a mistake in identifying the states. In this attack she measures all the quantum signals coming from Alice to Bob and based on her measurement results she prepares new signals that she sends to Bob.

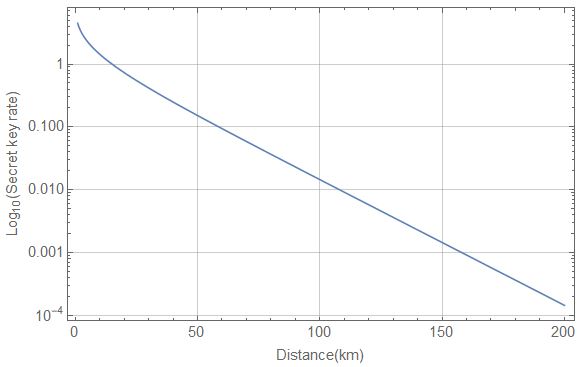
The evaluation of our attack appears in Figure 4, where one can see that the attack can provide better values for both of the monitored quantities (quantum bit error rate and the visibility that describes how the adjacent coherent laser pulses by Alice interfere with each other) than what can be achieved in the actual experiment, which makes it insecure.

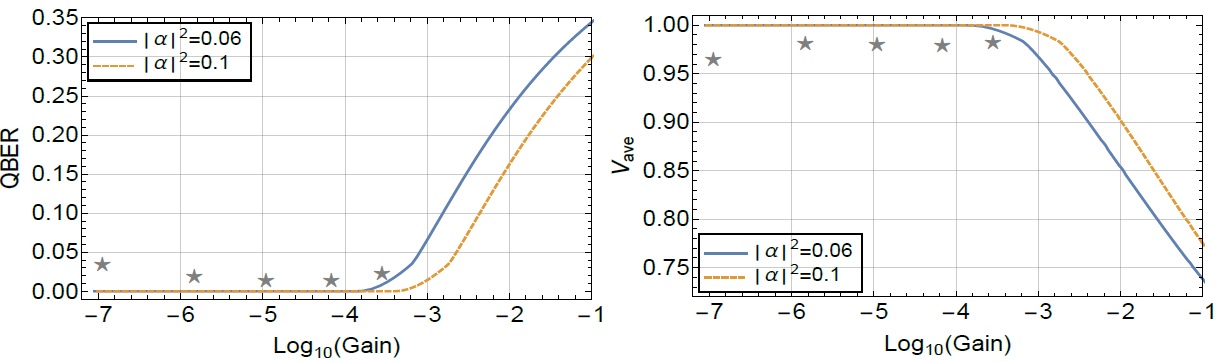
Figure 4. The stars represent the values achieved in the experiment, the curves represent the performance of our attack.The two different lines correspond to the two different intensity settings that Alice uses. The smaller gain values basically mean longer distances.

The most important consequence of our attack is that we showed that the secret key rate of the COW protocol is proportional to at most the square of the channel loss between the parties so its performance is much worse than what had been thought before.

Conclusions

We have seen that improving the performance of QKD protocols is an important task towards building a global quantum communication infrastructure for communications, which could be the remedy for the threat on the secrecy of our communications by future quantum computers. But at the same time it is a challenging task due to, for example, the difficulties attributed to theoretical limitations like the repeaterless bound or to the fact that the real-life devices used in an implementation are always imperfect. We have also seen that the popular COW protocol is not an appropriate candidate for long distance QKD.

Spotlight article, Story of the month

Story of the Month: Experimental Twin Field Quantum Key Distribution

29th January 2020 Mirko Pittaluga

The importance of secure digital communications

One aspect of everyday life that has been revolutionised the most in modern times is our ability to communicate easily and nearly instantaneously from and to almost any part of the world. Listing all the aspects of life that have been affected by this revolution woul

d be a challenging task. But, just to mention a few, think about how we communicate with our friends and loved ones, on how we access financial services (ATMs, chip-based credit cards, online bank accounts), and about how we communicate in the work place (emails or direct messaging systems). In all these cases, digital communications have deeply changed the way we behave.

MP_-_Number_of_devices_connected_to_internet — **Fig. 1:** Expected number of connected devices to the Internet. This chart is obtained from recent reports developed by both Cisco and Ericsson. Figure taken form this article.

A good way to assess our increasing dependence on digital communication tools is by looking at the increase in the number of internet connected devices over the recent years (Fig. 1). Their number has increased dramatically over the last decade, reaching tens of billions.

As for any new technology, these new means of communication

generate new problems and risks. Among the most critical is the difficulty of keeping our digital communications private and confidential. Security is a crucial requirement for many of our communications. And it is for this reasons that over the past 60 years a lot of effort has been put into the development of cryptography, i.e. the set of techniques that allow us to transmit and store information securely. It is thanks to cryptography that nowadays we can have private digital communications.

What is Quantum Key Distribution and why do we need it

Most of today’s digital communications are protected by public-key cryptographic schemes. The security of these is based upon two assumptions: there are certain mathematical problems that are very difficult (or almost impossible) to solve with (1) current day technology and (2) mathematical knowledge. These two assumptions looked extremely strong in late ’70s when public-key cryptography was first introduced, but unfortunately today this is no longer the case. In the mid-90’s it was demonstrated that, among other far-reaching capabilities, a powerful enough quantum computer could easily break the security of the currently deployed public-key cryptography schemes. This is a daunting prospect for the security

of our digital communications, especially given the recent impressive progress towards the construction of quantum computers.

The need for an alternative to the present cryptographic standards stimulated the research for a different approach to cryptography. One possible solution for this problem has been found in Quantum Key Distribution (QKD). The most interesting aspect of QKD is that its security is based upon a very different set of assumptions: the correctness of the law of physics (particularly quantum physics), and on the unflawed physical implementation of the devices used to set up the secure communication. There is a notable advantage with this approach: while advances in technology and limits to the mathematical knowledge are not under our control, the security of QKD is based upon something we have a more direct control of.

Limitations associated to QKD: cost, security and distance

Since its conception in 1984, the research around QKD advanced considerably, and reached remarkable results. We are now at a stage where this technology is practical enough to be implementable in real world scenarios and companies that sell ready-to-use QKD devices to the general public already exist.

Despite the recent progress in QKD development, a few limitations

associated with its implementation remain. The most relevant of which are:

the requirement of specifically designed hardware to perform QKD;
the cost of this hardware;
the security associated with its physical implementation;
the limited distance at which QKD operate run successfully.

Points 1 and 2 can probably be considered technical limitations. There is a lot of research addressing these issues, and much of it focuses on the miniaturisation of QKD devices into small form factors, compatible with scalable fabrication techniques and suitable for mass production. For more information on this argument, see the post by my colleague and fellow QCALL member, Innocenzo De Marco.

Points 3 and 4 are instead of a more fundamental nature.

The security of any QKD implementation relies on a perfect match between the theoretical model describing the system and its physical implementation. Therefore, in order to guarantee the perfect security of a system, two approaches are possible:

One is to develop theoretical models that consider all the possible experimental flaws (see the work of my fellow QCALL member Margarida Pereira to get an insight on this type of research).
The other one is to remove all the implementation flaws from the QKD device.

One of the most effective ways to implement this second approach happen to be the removal of the detectors from within the secure perimeter of the QKD system. This is the strategy used in Measurement Device Independent (or MDI) QKD protocols. These

types of protocol are considered more secure than the other QKD protocols because they are less prone to implementation security issues.

MP_-_Cropped_Keyrates_and_PLOB — **Fig. 2:** Key rate obtained in state of the art QKD experiments, over channel loss. All the points in the graph lie below the thick blue line which is the PLOB bound.

The fourth and final limiting factor of QKD is the maximum distance at which it can operate successfully. This is fundamentally limited by the information carriers used in QKD, which are (in the ideal case) single photons. It can be proved that with the current technology there is a fundamental limit on the maximum key rate that is achievable over a certain channel loss. This limit is often referred as the repeaterless secret key capacity bound (or PLOB bound, from the name of the researchers that discovered it) and scales linearly with the channel loss (Fig. 2). In practice, the maximum distance covered by QKD communications reaches only a few hundreds of kilometres.

The focus of my research is demonstrating that it is possible to increase the maximum attenuation at which QKD can be performed, while maintaining the highest standard of security by removing the detectors from the secure perimeter of the setup.

Twin Field QKD: protocol concepts and advantages

MP_-_TF-QKD_schematic_modified — **Fig 3:** Simple schematic of the setup for TF-QKD. Inspired by figure in this article.

At the beginning of 2018 a group of researchers at Toshiba Research

Europe Ltd. published a paper that introduced a novel QKD protocol called Twin Field QKD (or simply TF-QKD). The protocol has several interesting features, the most remarkable of which is that it introduces a viable way to overcome the PLOB bound with currently available technology. This result is very relevant from a practical point of view because it means that there is now a way to extend the maximum transmission distance achievable by QKD.

This result is possible thanks to a different way of encoding and retrieving the information in the quantum carriers used for the protocol. In TF-QKD the information is encoded in the phase of the optical pulses prepared by the two users that want to establish the secure communication, and the secret key is retrieved via a single photon interference measurement made by a user in the middle (see the simple schematic in Fig. 3). Another interesting aspect of TF-QKD is that it is also Measurement Device Independent, which means that it meets the strictest standards of security.

The advantages associated with this new encoding and detection strategy come at a price: TF-QKD introduces a series of new challenges that have to be faced for its implementation. The most difficult of which are:

The generation of twin optical fields from two space-separated laser sources;
The stabilisation of the channel used during the communication. This has to be stabilised to a new level of precision compared to other QKD protocols.

TF-QKD implementation

Mirko_Pittaluga_-_TF-QKD_Experimental_Setup — **Fig. 4:** Proof of principle TF-QKD experimental setup. Image courtesy of Mariella Minder.

The focus of my research within the QCALL network, has been to demonstrate the experimental feasibility of the TF-QKD protocol. For this purpose, together with my colleagues at Toshiba Research Europe Ltd., I developed the first TF-QKD setup, and proved that the protocol can indeed be used to overcome the PLOB bound.

The setup used for this task is shown in Fig. 4. It is important to notice that in this proof-of-principle experiment we simulated the channel attenuation associated with a long communication channel by means of Variable Optical Attenuators (VOAs, optical devices that set a chosen attenuation over an optical channel). This enabled us to execute the experiment at extremely high channel attenuations, without having to worry too much about the phase fluctuations that would have been introduced by long optical fibers.

The elements of novelty in this setup, compared to other QKD implementations, are the frequency distribution system (represented by the brighter purple box in Fig 4), and the system used for phase stabilisation. More information on these are given below.

The frequency distribution system: Optical Phase-Locked Loop

**Fig. 5:** Schematic of the OPLL setup.

A technique developed in classical optical communications was borrowed for the optical frequency distribution. With this technique, called Optical Phase Locked Loop (or OPLL), it is possible to force two lasers to emit at the same optical frequency. This is done by locking the interference beating between two lasers to a target frequency through a PID controller connected to an actuator. See Fig. 5 for a more detailed schematic of the OPLL implementation in our setup.

The quantum channel stabilisation

Since in TF-QKD the information that the users want to communicate is associated to the phase of optical that they prepare, it is fundamental to keep track of the phase fluctuations between the two users. In this experiment we have accomplished this by stabilizing the phase of the quantum channel to a fixed and known value. To achieve this, some reference pulses were interleaved into the phase encoded pattern, and a phase feedback system was developed. The phase feedback system was composed of a PID controller and a phase modulator.

Results and outlook

With this setup we were able to execute TF-QKD at different channel attenuations. We performed the protocol at several attenuation levels, spaced roughly by 10 dB, and extracted a secret key that could be used for a secure digital communication. The results of this experiment are shown in Fig. 6 (the points in the plot), alongside the simulation curves. Our experimental results align very well with the values predicted by the simulations.

After its introduction, a lot of interest arose around TF-QKD, and several protocol variants have been proposed since then. The different colours for the points in Fig. 6 represent different TF-QKD protocol variants tested with this experiment. Our experimental setup had the flexibility to implement 3 variants in total: the original TF-QKD protocol (in red in the graph), the Send-Not-Send TF-QKD protocol (blue points in the graph), and the CAL TF-QKD protocol (yellow point in the graph).

It is remarkable that for all these protocols we managed to obtain a positive key rate above the PLOB bound, overcoming experimentally the repeaterless secret capacity bound for the first time ever. We also note that for the original and the SNS protocols we achieved a positive key rate at unprecedentedly high channel attenuations, that would be equivalent to the losses introduced by more than 500 km of ultra-low loss fiber.

MP_-_TF-QKD_key_rate — **Fig 6:** Key rate generated by our TF-QKD system art different attenuations, for various TF-QKD variants.

This experiment was the first demonstration of the feasibility of the TF-QKD protocol, and the first experimental evidence that it is possible to overcome the secret key capacity bound with current day technology. This experiment can be considered the first realisation of an effective quantum repeater, as suggested by a recent review on the advances in quantum cryptography.

Mirko Pittaluga

QCALL

Quantum Communications for ALL