Category Archives: Story of the month

The importance of secure digital communications

One aspect of everyday life that has been revolutionised the most in modern times is our ability to communicate easily and nearly instantaneously from and to almost any part of the world. Listing all the aspects of life that have been affected by this revolution woul

d be a challenging task. But, just to mention a few, think about how we communicate with our friends and loved ones, on how we access financial services (ATMs, chip-based credit cards, online bank accounts), and about how we communicate in the work place (emails or direct messaging systems). In all these cases, digital communications have deeply changed the way we behave.

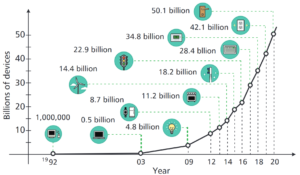
MP_-_Number_of_devices_connected_to_internet — **Fig. 1:** Expected number of connected devices to the Internet. This chart is obtained from recent reports developed by both Cisco and Ericsson. Figure taken form this article.

A good way to assess our increasing dependence on digital communication tools is by looking at the increase in the number of internet connected devices over the recent years (Fig. 1). Their number has increased dramatically over the last decade, reaching tens of billions.

As for any new technology, these new means of communication

generate new problems and risks. Among the most critical is the difficulty of keeping our digital communications private and confidential. Security is a crucial requirement for many of our communications. And it is for this reasons that over the past 60 years a lot of effort has been put into the development of cryptography, i.e. the set of techniques that allow us to transmit and store information securely. It is thanks to cryptography that nowadays we can have private digital communications.

What is Quantum Key Distribution and why do we need it

Most of today’s digital communications are protected by public-key cryptographic schemes. The security of these is based upon two assumptions: there are certain mathematical problems that are very difficult (or almost impossible) to solve with (1) current day technology and (2) mathematical knowledge. These two assumptions looked extremely strong in late ’70s when public-key cryptography was first introduced, but unfortunately today this is no longer the case. In the mid-90’s it was demonstrated that, among other far-reaching capabilities, a powerful enough quantum computer could easily break the security of the currently deployed public-key cryptography schemes. This is a daunting prospect for the security

of our digital communications, especially given the recent impressive progress towards the construction of quantum computers.

The need for an alternative to the present cryptographic standards stimulated the research for a different approach to cryptography. One possible solution for this problem has been found in Quantum Key Distribution (QKD). The most interesting aspect of QKD is that its security is based upon a very different set of assumptions: the correctness of the law of physics (particularly quantum physics), and on the unflawed physical implementation of the devices used to set up the secure communication. There is a notable advantage with this approach: while advances in technology and limits to the mathematical knowledge are not under our control, the security of QKD is based upon something we have a more direct control of.

Limitations associated to QKD: cost, security and distance

Since its conception in 1984, the research around QKD advanced considerably, and reached remarkable results. We are now at a stage where this technology is practical enough to be implementable in real world scenarios and companies that sell ready-to-use QKD devices to the general public already exist.

Despite the recent progress in QKD development, a few limitations

associated with its implementation remain. The most relevant of which are:

the requirement of specifically designed hardware to perform QKD;
the cost of this hardware;
the security associated with its physical implementation;
the limited distance at which QKD operate run successfully.

Points 1 and 2 can probably be considered technical limitations. There is a lot of research addressing these issues, and much of it focuses on the miniaturisation of QKD devices into small form factors, compatible with scalable fabrication techniques and suitable for mass production. For more information on this argument, see the post by my colleague and fellow QCALL member, Innocenzo De Marco.

Points 3 and 4 are instead of a more fundamental nature.

The security of any QKD implementation relies on a perfect match between the theoretical model describing the system and its physical implementation. Therefore, in order to guarantee the perfect security of a system, two approaches are possible:

One is to develop theoretical models that consider all the possible experimental flaws (see the work of my fellow QCALL member Margarida Pereira to get an insight on this type of research).
The other one is to remove all the implementation flaws from the QKD device.

One of the most effective ways to implement this second approach happen to be the removal of the detectors from within the secure perimeter of the QKD system. This is the strategy used in Measurement Device Independent (or MDI) QKD protocols. These

types of protocol are considered more secure than the other QKD protocols because they are less prone to implementation security issues.

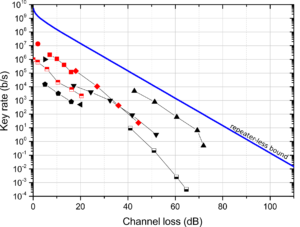
MP_-_Cropped_Keyrates_and_PLOB — **Fig. 2:** Key rate obtained in state of the art QKD experiments, over channel loss. All the points in the graph lie below the thick blue line which is the PLOB bound.

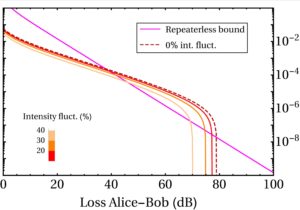
The fourth and final limiting factor of QKD is the maximum distance at which it can operate successfully. This is fundamentally limited by the information carriers used in QKD, which are (in the ideal case) single photons. It can be proved that with the current technology there is a fundamental limit on the maximum key rate that is achievable over a certain channel loss. This limit is often referred as the repeaterless secret key capacity bound (or PLOB bound, from the name of the researchers that discovered it) and scales linearly with the channel loss (Fig. 2). In practice, the maximum distance covered by QKD communications reaches only a few hundreds of kilometres.

The focus of my research is demonstrating that it is possible to increase the maximum attenuation at which QKD can be performed, while maintaining the highest standard of security by removing the detectors from the secure perimeter of the setup.

Twin Field QKD: protocol concepts and advantages

MP_-_TF-QKD_schematic_modified — **Fig 3:** Simple schematic of the setup for TF-QKD. Inspired by figure in this article.

At the beginning of 2018 a group of researchers at Toshiba Research

Europe Ltd. published a paper that introduced a novel QKD protocol called Twin Field QKD (or simply TF-QKD). The protocol has several interesting features, the most remarkable of which is that it introduces a viable way to overcome the PLOB bound with currently available technology. This result is very relevant from a practical point of view because it means that there is now a way to extend the maximum transmission distance achievable by QKD.

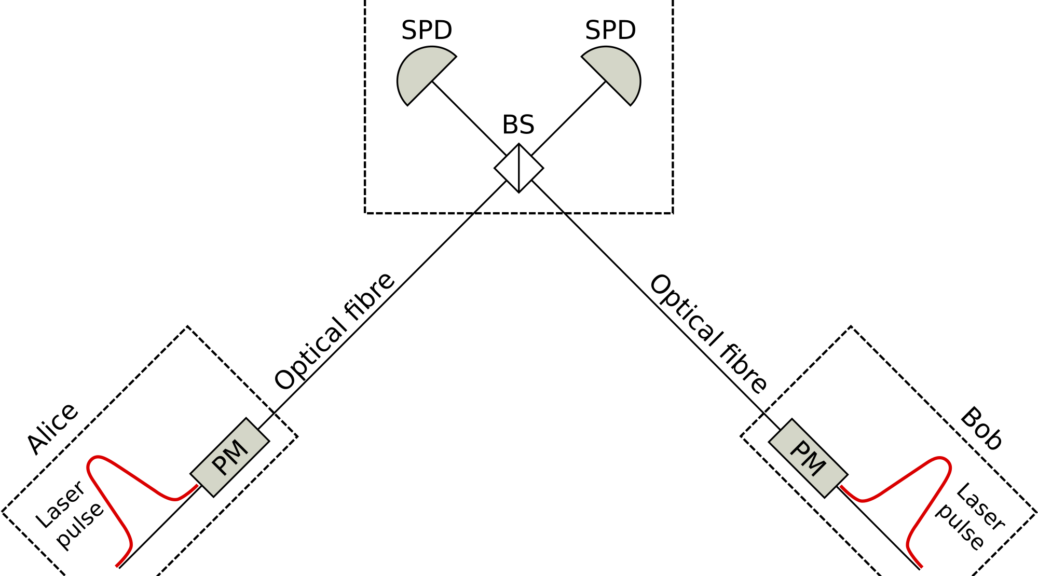
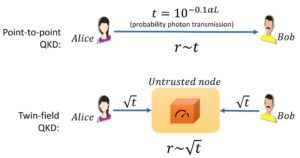
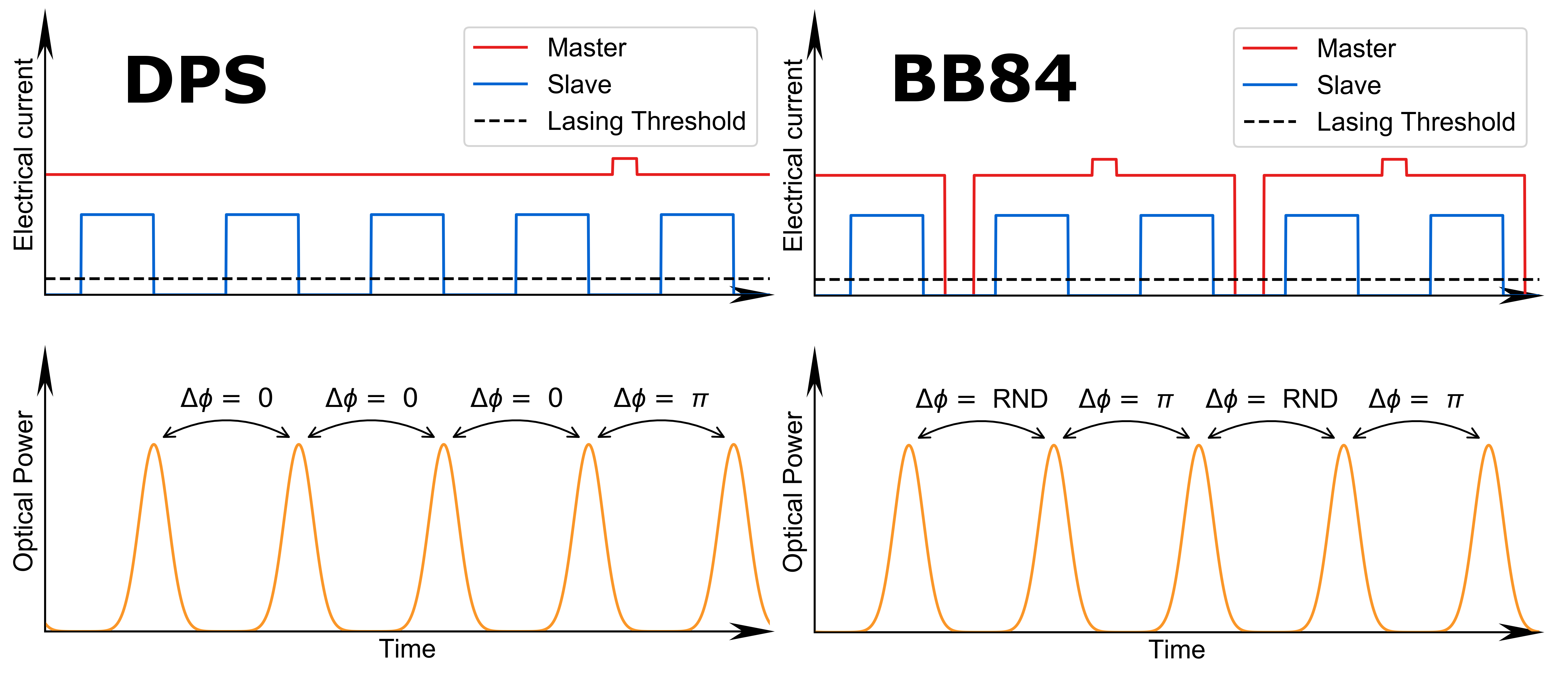
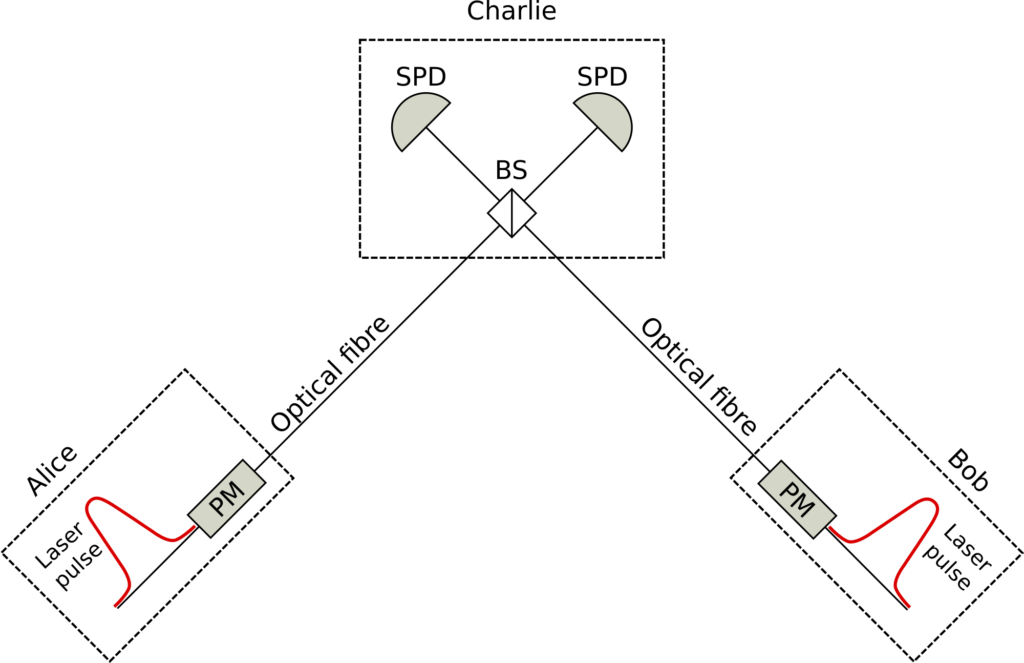
This result is possible thanks to a different way of encoding and retrieving the information in the quantum carriers used for the protocol. In TF-QKD the information is encoded in the phase of the optical pulses prepared by the two users that want to establish the secure communication, and the secret key is retrieved via a single photon interference measurement made by a user in the middle (see the simple schematic in Fig. 3). Another interesting aspect of TF-QKD is that it is also Measurement Device Independent, which means that it meets the strictest standards of security.

The advantages associated with this new encoding and detection strategy come at a price: TF-QKD introduces a series of new challenges that have to be faced for its implementation. The most difficult of which are:

The generation of twin optical fields from two space-separated laser sources;
The stabilisation of the channel used during the communication. This has to be stabilised to a new level of precision compared to other QKD protocols.

TF-QKD implementation

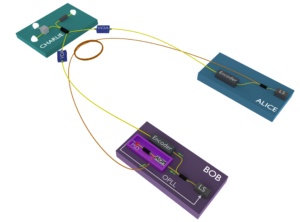
Mirko_Pittaluga_-_TF-QKD_Experimental_Setup — **Fig. 4:** Proof of principle TF-QKD experimental setup. Image courtesy of Mariella Minder.

The focus of my research within the QCALL network, has been to demonstrate the experimental feasibility of the TF-QKD protocol. For this purpose, together with my colleagues at Toshiba Research Europe Ltd., I developed the first TF-QKD setup, and proved that the protocol can indeed be used to overcome the PLOB bound.

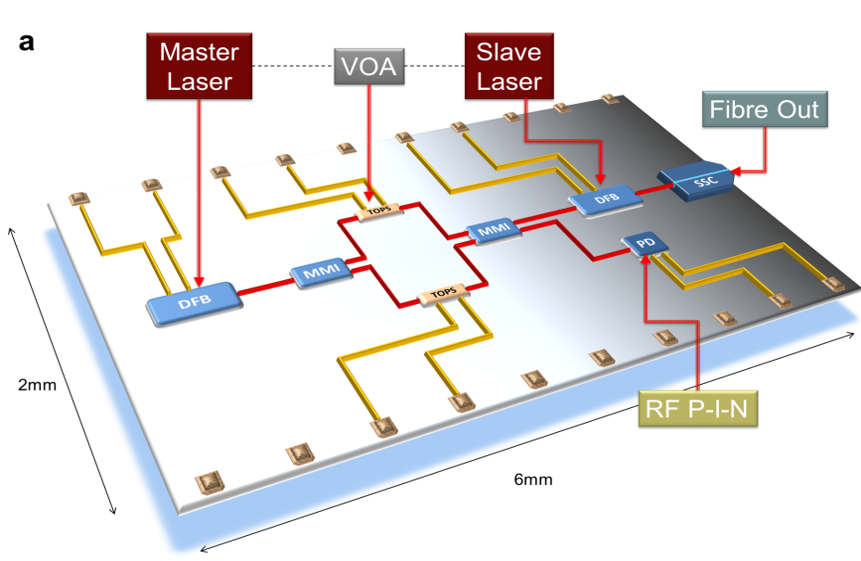
The setup used for this task is shown in Fig. 4. It is important to notice that in this proof-of-principle experiment we simulated the channel attenuation associated with a long communication channel by means of Variable Optical Attenuators (VOAs, optical devices that set a chosen attenuation over an optical channel). This enabled us to execute the experiment at extremely high channel attenuations, without having to worry too much about the phase fluctuations that would have been introduced by long optical fibers.

The elements of novelty in this setup, compared to other QKD implementations, are the frequency distribution system (represented by the brighter purple box in Fig 4), and the system used for phase stabilisation. More information on these are given below.

The frequency distribution system: Optical Phase-Locked Loop

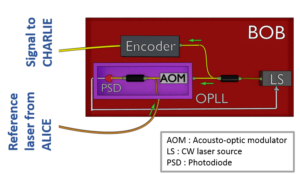
**Fig. 5:** Schematic of the OPLL setup.

A technique developed in classical optical communications was borrowed for the optical frequency distribution. With this technique, called Optical Phase Locked Loop (or OPLL), it is possible to force two lasers to emit at the same optical frequency. This is done by locking the interference beating between two lasers to a target frequency through a PID controller connected to an actuator. See Fig. 5 for a more detailed schematic of the OPLL implementation in our setup.

The quantum channel stabilisation

Since in TF-QKD the information that the users want to communicate is associated to the phase of optical that they prepare, it is fundamental to keep track of the phase fluctuations between the two users. In this experiment we have accomplished this by stabilizing the phase of the quantum channel to a fixed and known value. To achieve this, some reference pulses were interleaved into the phase encoded pattern, and a phase feedback system was developed. The phase feedback system was composed of a PID controller and a phase modulator.

Results and outlook

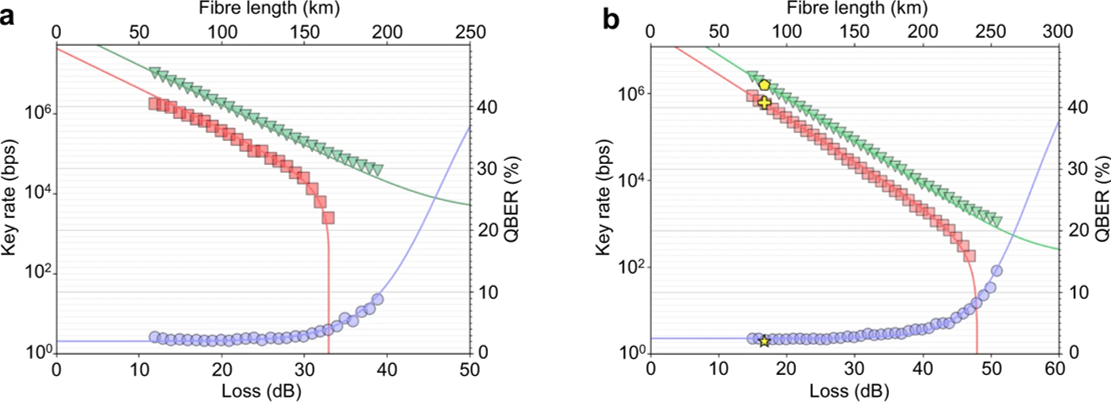
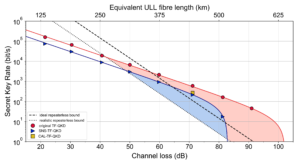
With this setup we were able to execute TF-QKD at different channel attenuations. We performed the protocol at several attenuation levels, spaced roughly by 10 dB, and extracted a secret key that could be used for a secure digital communication. The results of this experiment are shown in Fig. 6 (the points in the plot), alongside the simulation curves. Our experimental results align very well with the values predicted by the simulations.

After its introduction, a lot of interest arose around TF-QKD, and several protocol variants have been proposed since then. The different colours for the points in Fig. 6 represent different TF-QKD protocol variants tested with this experiment. Our experimental setup had the flexibility to implement 3 variants in total: the original TF-QKD protocol (in red in the graph), the Send-Not-Send TF-QKD protocol (blue points in the graph), and the CAL TF-QKD protocol (yellow point in the graph).

It is remarkable that for all these protocols we managed to obtain a positive key rate above the PLOB bound, overcoming experimentally the repeaterless secret capacity bound for the first time ever. We also note that for the original and the SNS protocols we achieved a positive key rate at unprecedentedly high channel attenuations, that would be equivalent to the losses introduced by more than 500 km of ultra-low loss fiber.

MP_-_TF-QKD_key_rate — **Fig 6:** Key rate generated by our TF-QKD system art different attenuations, for various TF-QKD variants.

This experiment was the first demonstration of the feasibility of the TF-QKD protocol, and the first experimental evidence that it is possible to overcome the secret key capacity bound with current day technology. This experiment can be considered the first realisation of an effective quantum repeater, as suggested by a recent review on the advances in quantum cryptography.

Mirko Pittaluga

Spotlight article, Story of the month

Story of the Month: Quantum Conferencing

27th January 2020 Federico Grasselli

Federico works on theoretical progress in multi-party quantum key distribution, also known as quantum conferencing. Have you ever heard about it?

Your data is under threat

In recent times people, as well as institutions, companies and governments, are increasingly concerned about the privacy of their data and are constantly looking for better ways to keep it safe.

One of the instances in which private data becomes vulnerable is when it is transmitted from one party to another one (e.g. a bank and its customer, the secret services and the government, etc.). In order to keep the data safe, the sender encrypts the data with a secret key -the encryption key- that he/she shares with the receiver, prior to transferring it. The receiver then decrypts the data using the same secret key. A potential eavesdropper cannot learn the data without the encryption key. Hence, the data is secure as far as the key shared by the sender and the receiver through a cryptographic scheme is secret.

Classical Cryptography

Nowadays, the standard cryptographic schemes in use are referred to by quantum physicists in my field as “classical cryptography“. The security of such schemes relies on assumptions on the adversary’s computational capabilities , thus being vulnerable to retroactive attacks. In other words, an adversary could intercept and store the data encrypted by a classical crypto scheme, waiting to have sufficient computational power to decipher it. The recent developments of quantum computers, which promise unprecedented computational power, further increase the vulnerability of classical cryptography.

Quantum key distribution is the cure

QKD scheme

Quantum theory, despite being a threat to current cryptographic schemes, also provides a solution. Indeed, the mentioned security concerns and the prospect of commercialization boosted major advancements in the field of quantum cryptography and particularly in quantum key distribution (QKD).

A QKD protocol enables two parties, Alice and Bob, to generate a shared secret key by sending quantum systems (typically photons of light) through a quantum channel that can be under the control of the eavesdropper (Eve), and by measuring the systems upon reception. Alice and Bob are also equipped with an authenticated public channel, e.g. a phone call wiretapped by Eve.

By relying on intrinsic properties of quantum theory, QKD can be unconditionally secure regardless of the eavesdropper’s computational capabilities, unlike classical cryptography. This remarkable feature of QKD allows for ever-lasting secure communication and attracted the attention of companies, private institutions and governments.

QKD has been successfully implemented over 400 km of optical fibers and over 1000 km of satellite-to-ground links, and has already reached the market with companies like Toshiba and ID Quantique.

What makes QKD secure?

The unconditional security offered by QKD is based on distinctive quantum features, such as entanglement. When two or more quantum systems are entangled, their properties are strongly interconnected. Indeed, measuring a property on one quantum system immediately determines the measurement outcome of the same property on the other systems. This fact can be used to generate correlated outcomes when different parties perform the same measurement on their entangled quantum systems. The correlated outcomes can then be used as a shared key.

monogamy of entanglement

The key generated in this way is secret thanks to the monogamy of entanglement. According to this peculiar feature of entanglement, if two parties are strongly entangled, a third party shares little entanglement with them. The entangled parties can thus obtain a shared key with their highly correlated measurement outcomes while being sure that the third party -a potential eavesdropper- has little information about it.

Quantum conferencing

NQKD

The task of QKD can be generalized to more than two parties through a conference key agreement (CKA), where the goal is the establishment of a shared secret key -a conference key– among several parties. The conference key can then be used by one party to securely broadcast a message to the remaining parties.

The CKA could be trivially realized by performing bipartite QKD schemes between pairs of parties and using the established keys to distribute the conference key. Alternatively, one can exploit the correlations arising in multi-partite entangled states and devise a CKA protocol which directly outputs a secret conference key. Such truly multi-partite schemes are a natural application of quantum networks and have been proven to be advantageous in certain network configurations and noise regimes. In this post we focus on the latter type of CKA (the first review on this research topic [“Quantum Conference Key Agreement: A Review”, Murta, Grasselli, Kampermann and Bruss, 2020] is going to be published shortly).

The multiparty BB84 protocol

The BB84 protocol, devised by Bennett and Brassard in 1984, is the first and arguably the most famous of all the QKD protocols. Due to its simplicity, variants of the protocol have been widely implemented and even commercialized.

In our first work in the QCALL network, we generalized the BB84 protocol to a scenario with an arbitrary number of parties “N” willing to share a conference key, obtaining the so called N-BB84 protocol. Based on our work, an upcoming experimental implementation of a four-party BB84 protocol is about to be published [Proietti, Ho, Grasselli, Barrow, Malik, Fedrizzi, 2020].

The security proof of most QKD protocols is initially performed in a simplistic scenario, i.e. when the parties exchange an infinite number of quantum signals (asymptotic scenario). This is, of course, far from reality but it greatly simplifies the proof and gives indication on the protocol’s real-life performance.

N-BB84-vs-N-sixstate

A more realistic security proof with a finite number of signals (finite-key scenario), must consider that the measured data in the execution of the protocol is affected by statistical fluctuations. The challenge is to guarantee unconditional security of the distilled secret key despite the statistical fluctuations affecting the data.

In our work, we proved the security of the N-BB84 protocol and of another existing multiparty protocol (the N-six-state protocol) in the finite-key scenario, when the eavesdropper is allowed to perform the most general attack on the quantum channels (coherent attack). We also compared the performances of the two protocols under realistic conditions and showed that the N-BB84 protocol requires a lower number of protocol rounds to produce a non-null secret key.

Achieving longer distances

TF scheme

Most of the early QKD protocols do not rely on any intermediate relay: the parties taking part to the protocol are connected by a single-piece quantum channel. Such protocols are often called point-to-point schemes.

In spite of the great distances experimentally achieved by point-to-point QKD protocols (see above), their key rates are fundamentally limited. The key rate “r” of a QKD protocol is given by the number of secret key bits per protocol round (in a round one or more parties send a quantum signal) and its value is typically well below 1. Clearly, in any point-to-point QKD scheme the key rate cannot exceed the probability “t” that the signal sent by Alice reaches Bob.

The problem is that most QKD protocols employ photons as information carriers and the probability “t”of a photon traveling the distance “L” separating Alice from Bob decreases exponentially with “L” ! (see figure) Thus, key rates of point-to-point QKD schemes decrease exponentially with the distance, strongly constraining their long-distance applicability.

A solution to this limitation is provided by the recently-developed twin-field (TF) QKD protocol, initially introduced by our QCALL partners in Toshiba. In TF QKD, Alice and Bob prepare weak coherent pulses corresponding to a random bit they picked and send them to a central untrusted relay. The relay combines the pulses, measures them, and announces the measurement outcome. Based on the outcome, Bob either flips his bit or does nothing, in order to match it with Alice’s. By repeating this procedure at every round, the parties establish a secret key, which cannot be retrieved by the untrusted relay, even with the information of the measurement outcomes.

Being TF-QKD based on single-photon interference events occurring in the untrusted node, only one photon out of the two sent by Alice and Bob needs to arrive at the central relay at every round. Thus, the key rate of TF-QKD scales with the probability that one photon covered half of the total channel length (square root of “t”). This implies a square-root improvement in the performance over point-to-point QKD protocols, allowing to reach longer distances.

TF-QKD is currently the only experimentally implemented protocol with an improved scaling of the key rate versus the distance, making it the new benchmark for far-distance QKD.

contour_plot 3 decoys intensity fluct

With a first and a second publication in collaboration with our QCALL colleagues in Vigo, we investigated the practical performance of the TF QKD protocol proposed by Curty et al. In particular, we optimized its key rate when the distances separating Alice and Bob from the untrusted node differ and showed that the protocol can achieve good key rates even in extremely asymmetric scenarios. We also showed that the protocol is robust against intensity fluctuations affecting the parties’ lasers (figures above).

W state vs NBB84

Inspired by the TF-QKD protocol, we extended its founding idea to the multiparty scenario. We introduced a CKA where N parties simultaneously establish a conference key by relying again on single-photon interference. The protocol, also called “W state protocol”, presents a remarkable improvement in the key rate-vs-distance compared to its point-to-point couterpart, just like TF-QKD (see figure).

Indeed, in the W state protocol just one photon out of the N photons sent by every party needs to arrive at the central relay, while in point-to-point multiparty protocols like the N-BB84 (and N-six-state), each of the N photons must be successfully transmitted. We proved the security of the W state protocol in the finite-key regime and for general attacks.

For the security paranoids

QKD offers an exceptional level of security, provided that the assumptions on the devices used for its implementation are experimentally verified. However, the devices could be affected by imperfections difficult to characterize, or, much worse, they could be forged by the eavesdropper in order to learn the secret key. Therefore, it is challenging to ensure that the assumptions on the implementation of a QKD protocol are met in practice.

DIQKD

Fortunately, device-independent (DI) QKD can guarantee the same level of security independently of the actual functioning of the employed devices. In this framework, the devices used by the parties are modeled as black boxes (i.e. completely uncharacterized) producing an output upon receiving an input from the party. The parties collect a series of outputs (with correspondent inputs) by repeating the same procedure for several rounds, making sure that they are distant enough so that no signal can travel from their device to the other’s device. If the collected data cannot be explained by a local deterministic strategy (for which a third party in the middle instructs the devices on the output to produce), the parties conclude that their data exhibits non-local correlations. This means that it was produced by an entangled state shared by Alice and Bob’s devices. Thanks to the monogamy of entanglement, the secrecy of the parties’ correlated outcomes is restored, guaranteeing that the key distilled from the outputs is secret.

We are currently working on a project which aims at devising new and better-performing device-independent multiparty QKD protocols, in short: DICKA. The fundamental principle on which these protocols are based would be the same, just extended to more than two parties.

If you want to know how this will turn out, stay tuned!

Spotlight article, Story of the month

Story of the month: Chip-based technologies for Quantum Communications

3rd September 2019 Innocenzo De Marco 1 Comment

The need for Quantum Communications

The rise of quantum computers will break public key cryptography and consequently render obsolete existing secure communication infrastructures our modern society relies upon. This imminent threat prompts development of new counter technologies, and one of the most promising candidates is quantum communication. Quantum physics provides the ideal background to work with, due to the inherent uncertainty of quantum properties. Such uncertainty is crucial to generate randomness, which is the main ingredient of secure communications.

Quantum Key Distribution

Quantum Key Distribution (QKD) is one of the several ideas which exploit quantum randomness. Generating an encryption key, shared between two parties and unknown to any attackers, is the goal of the different QKD protocols. The security of the generated key is guaranteed by the laws of quantum physics: an eavesdropper can not do better than just guess the encryption key, no matter their computational power.

The BB84 protocol was the very first QKD protocol, introducing for the first time the idea of using the quantum states of photons to distribute a key between two parties. After that, a myriad of new protocols were proposed, each with their own advantages and disadvantages. The underlying concept, however, remains unchanged: one of the two parties, Alice, sends the other, Bob, a random sequence of bits encoded in a quantum property of a train of photons (polarisation, phase, time); an eavesdropper intercepting the signal inevitably disturbs the quantum state and, consequently, introduces noise at the receiving end that will highlight the presence of eavesdropping.

Since that first proposal in 1984, QKD has attracted a great deal of interest in the scientific community. Its experimental implementations have improved substantially: the communication distance has risen from a mere 32cm in free space in the very first QKD experiment, to 421km of optical fibre in a recent demonstration. This impressive distance can even be extended much further with the newly discovered TF-QKD protocol (which will be covered in the next story of the month).

QKD has gained popularity outside academia as well, with companies like QCALL partners Toshiba and ID Quantique developing their own QKD systems.

Chip-based QKD

Large-scale deployment of QKD systems is yet to become a reality. One of the obstacles is that existing QKD equipment is space and power consuming, and very expensive.

To mitigate these constraints and ease the QKD path to market, it is necessary to miniaturise and mass-produce the QKD devices. This is the main focus of QCALL project #1, aiming at the development of integrated photonic devices for Quantum Communications.

Integrated Photonics

Photonic Integrated Circuits (PICs) are already a widespread technology in classical communications. They have the capability of embedding a plethora of optical components on a very small form factor device.

Chip-Finger — An InP chip with lasers, modulators and output waveguides. Such elements integrated on a chip sit on the top of a fingertip, whereas they would result in a 40 to 50 times bigger setup using ordinary components.

In addition to this, mass production of photonic chips is significantly cheaper than assembling from discreet, bulky components, thanks to generic integration technology and multi-project wafers: like with electronic printed circuit boards, the foundries release a set of basic building blocks, which their clients will assemble to make their own circuits. This way, all components can be grown and processed on a wafer monolithically, i.e. in a single run: this allows for multiple circuits to be implemented at the same time, drastically lowering development and production costs for both the foundry and their clients.

Chip-based quantum communications

Integrated photonics seems the natural choice for nxet’generation Quantum Communications devices since their performance is well established in classical communications.

Among the building blocks needed for a QKD transmitter, there are lasers, waveguide couplers, phase modulators and photodiodes. All these can easily be implemented on a chip, and indeed there are several examples of chip-based devices implementing QKD protocols.

Our goal at Toshiba is to make smaller, cheaper and more efficient QKD devices based on photonic integration.

Chip-based quantum communications at Toshiba

Chip-based Quantum Random Number Generator

In order to correctly implement any QKD protocol, a prerequisite is that the initial bit sequence, sent from Alice to Bob, has to be truly random, otherwise an eavesdropper could exploit correlations among the bits to guess the bit sequence.

Generating true randomness is difficult and even fundamentally impossible by only classical means. The deterministic laws of electrodynamics always deliver a predictable outcome, in principle. However, the outcome becomes different in quantum physics. In our Quantum Random Number Generator (QRNG), we generate pulses from two independent laser and have them interfere on a beam splitter. The spontaneous emission process triggering the lasing action is of quantum nature. This guarantees that the phase of the optical pulses emitted by the lasers is inherently random. Hence, when the two pulses interfere, their interference amplitude is not predictable and we can use it to extract random numbers.

Layout of our Quantum Random Number Generator chip. DC: Direct Current; RF: Radio Frequency; VOA: Variable Optical Attenuator; MMI: Multi-Mode Interferometer; PD: Photodiode.

The novelty of our QRNG, as shown in this JOSA B paper, is in its plug-and-play format: as soon as it is assembled, it is ready to be used. All the optical components (the two lasers and a photodiode to detect the interfering pulses) are embedded onto a 6x2mm photonic chip, which is then connected to bespoke electronics. This is composed of an analog-to-digital converter reading the analog signal of the photodiode, and an FPGA that will post-process the data by removing any remaining information that an adversary can use. As an additional check, we ran the NIST test suite on subsets of our generated numbers, and observed that they passed all 17 tests. The output string of random numbers can then be used as input for the QKD modules.

A modulator-free quantum key distribution transmitter chip

The random key obtained from the QRNG is fed into a QKD transmitter. The transmitter chip developed by Toshiba removes the need for power-hungry phase modulators by the use of Master-Slave paired lasers. The information is encoded in the phase difference between pulses from the Slave laser, and can then be decoded by a receiving interferometer.

The working principle of the transmitter is based on combining the well-known phenomena of direct phase modulation and optical injection locking, both techniques already in use in classical optical communications. The idea of combining them for Quantum Communications was first introduced by Toshiba in 2016.

Direct phase modulation, as the name suggests, exploits the fact that the phase of a laser’s output is directly related to its driving signal: modulating such electrical current allows direct control over the phase of light emitted by a laser.

Optical injection locking is a phenomenon where one laser, namely the Master, injects light into a second, Slave, laser. This will cause the light from the Master to trigger emission from the Slave laser: light emitted from the Slave will then be “locked” to the same properties, in particular the same phase, as the injected light.

Combining these two techniques, we can then generate pulses from the Slave laser that will feature the phase we want to encode by modulating the Master.

Modulation for the DPS (left) and BB84 (right) protocols

This removes the need for phase modulators, which are extremely power consuming, while still allowing us to encode all the relevant information in our photons.

Implementing this setup into a photonic chip results in a versatile, compact QKD transmitter. Our QKD chip was tested in an experiment that is described in this npj Quantum Information paper.

The simple layout of our device allows us to achieve results in line with state-of-the-art bulk implementations for both the BB84 and the DPS protocol.

Results QKD chip — Performance of our QKD chip for the DPS (left) and BB84 (right) protocols. The blue lines represent QBER, the green lines represent the raw counts from the detectors, the red lines represent the secure key rates. The fibre length assumes an equivalent loss of 0.2 dB/km. The yellow markers indicate points obtained on a real fibre link.

This shows that our devices are suitable for being implemented into QKD systems. The small form factor and the lower cost associated with the generic integration process, combined with the lack of phase modulators, make our QKD chips a candidate for large-scale implementation of Quantum Communication systems.

Story of the month

Story of the month: Solid state crystals for quantum repeaters

15th August 2019 Antonio Ortu

Antonio works on Solid state crystals for quantum repeaters, do you like to know more? Please continue to read!

Quantum physics has some peculiar properties which can enhance the security and privacy of long-distance communication, a topic very relevant today and likely to become even more so in the near future. Moreover, quantum computers will need to be connected in a way compatible with their quantum nature. This is why preparing the ground for an implementation of quantum communication over future quantum networks is among the goals of the QCALL project. This task includes working on the physical devices that one day will make a quantum network functional.

Actually, the backbone of a quantum network already exists. Optical fibres are extensively used for high speed internet connection, and this is no coincidence. Light is an excellent carrier of information, given its speed that no other particle can reach, and it can be easily manipulated with modern technology, especially thanks to the laser. In addition, photons are among the most versatile physical systems in which a quantum state can be created, controlled and transferred. It seems only logical to exploit the existing fibre network to transmit also quantum states.

Quantum memories and repeaters

However, the present network is not ready yet for quantum communication. One of the reasons is that the quantum state of a photon is more fragile than the classical analogue of a simple pulse of light. Optical fibres are not perfect, and loss of information becomes a serious problem when speaking of long distances. In a state-of-the-art optical fiber, half of the photons in a laser pulse are lost every 17 km. While for classical information this can be compensated by repeater stations, where light pulses are amplified, this is not possible with quantum states as a consequence of the more fundamental no-cloning theorem.

We therefore need to rethink the concept of quantum repeater and adapt it to the rules of quantum physics. So far, several protocols have been proposed which exploit another feature typical of the quantum world: entanglement. In simple words, two or more particles are said to be entangled when they exist in a global state that cannot be simply described as a product of the states of the individual particles. A consequence of the entanglement is that interacting with one of these particles will also affect the result of any measurement of the properties of the others, which can be used for instance to prove the security of a communication channel. A quantum repeater then needs to be able to distribute entangled states between the network nodes, but also store these states in order to maintain a link with a node active for some time and allow the synchronization of multiple direct links that will finally connect the nodes at the extreme ends of the channel.

This is where quantum memories enter the game. At the core of a quantum repeater, these devices interact with incoming photons, store their state in some internal degrees of freedom, and release it after some time that can be chosen on-demand. All this while preserving the quantum properties of the stored state, including the entanglement with other photons and nodes of the network.

This is how a first quantum network might look. Links on the ground could also be integrated with satellite technology for intercontinental communication.

The quest for better memories

My task in the QCALL project, and as a PhD student in the group supervised by Mikael Afzelius at the University of Geneva in Switzerland, is to work on the practical side of the implementation of a quantum repeater, in particular by studying some novel candidate materials for quantum memories and to demonstrate storage of entanglement in such memories. Several physical systems have been proposed already for the purpose, most of them relying on groups (or more properly, ensembles) of atoms that can collectively interact with photons and potentially store the information they carry in their internal degrees of freedom. The strength of using a collection of many atoms is that, like a team, they can work together to enhance the probability that incoming photons will interact with any of them, and together keep trace of the information stored until the moment is chosen for it to be released as another photon. Another great advantage of ensemble-based memories is that an ensemble of atoms can store many photons at a time, and this multiplexing ability is key in order to reach reasonable communication rates. Here in Geneva we decided to work with a specific family of atoms, called rare earth elements, embedded in solid state crystals.

Rare earth elements are, despite the name, relatively common in the Earths’ crust and used widely in modern technology. For instance, one can find them in tv screens, smartphones and computer components. But how can they be useful in our quest for a quantum memory?

Examples of rare earth elements, with the most successful in quantum memories research highlighted in blue. — Examples of rare earth elements, with the most successful ones in quantum memories research highlighted in blue.

Advantages and challenges

As mentioned before, a quantum state is a delicate thing, be it a photon or an ensemble of rare earth ions in a crystal. Even if one manages to prepare a quantum state in a particle, in normal conditions it won’t last long. Most probably, our particle will interact with its environment very quickly, modifying the state in unpredictable ways. This is why, in our system, rare earth ions are embedded in specific types of crystals, which contain mostly elements that interact only weakly with the ions themselves or with the environment, on the condition that their temperature is of just few Kelvin above absolute zero, which is easily obtained with commercially available cryostats.

But how can we make sure our system is resilient to perturbations? A way of quantifying this is to measure the coherence lifetime: in other words, for how long our group of ions can keep working as a team in preserving the stored information without them “losing coherence” between themselves and with respect to the intial state of the photon absorbed. This is the crucial metric for a system to be able to preserve a quantum state.

When cooled, rare earth ions can easily record coherence lifetimes ranging from hundreds of microseconds to even a few seconds, depending on the specific element. This numbers might sound small, but from the point of view of a photon it’s actually a lot: to give an idea, in 100 microseconds a photon covers about 20 km in an optical fibre! However, a long coherence lifetime is not the only property we need. Other questions we have to answer are: is the colour (or frequency) of the light we want to use for communication compatible with our ions? How much information can we store in a given timeframe (multiplexing and bandwidth)? Can a state of light be efficiently absorbed and re-emitted without being distorted?

Unfortunately, so fare none of the physical systems proposed as a quantum memory can answer affirmatively to all these questions at the same time. In the specific case of rare earths, for instance, erbium is the most compatible with the infrared photons that are currently used in telecommunications (1500 nm of wavelength), but it suffers from high sensitivity to external perturbations. Praseodymium is very efficient in absorbing photons, but mainly for red light (600 nm), and its coherence lifetime is good but far from the best. Europium is very resistant to perturbations, but it is also much less efficient than praseodymium, and again at the wrong colour (yellow, 580 nm).

All these issues are being tackled with constant progress by various groups of researchers around the globe. For example, frequency conversion can solve the “wrong colour” problem at a price in efficiency; optical cavities can help the efficiency, but also reduce the bandwidth; and other techniques involving active control of the ions’ environment can reduce their sensitivity to perturbations and increase the effective coherence time, while adding more complexity to the storage protocol and demanding more resources. In any case, the exploration of new materials that can help improve all these aspects is still ongoing.

Our new entry: ytterbium

This is what the first part of my PhD was about. We studied a relatively unexplored rare earth element, ytterbium, in a host crystal called yttrium orthosilicate (YSO in short). It absorbs in the near infrared (980 nm), but its main strength, to begin with, is the bandwidth. Its electrons and nucleus can be addressed with photons at several frequencies, a bit like a cabinet with multiple shelves, which are well separated by at least half a GHz. This ultimately sets the bandwidth limitation of the memory! This is an advantage with respect to many of the most successful rare earths so far, for which this range is limited to tens of MHz of bandwidth only! (as in europium and praseodymium). In principle, increasing the bandwidth of the memory will lead to a larger operating speed of the repeater, and thus a faster connection rate in a quantum network.

The big unknown was the coherence lifetime. But we unexpectedly discovered that ytterbium can reach more than 1 ms if we choose to store a light pulse in specific internal states, created by an interplay of the intrinsic property of electrons and nuclei, called spin. At first this was very surprising, since usually materials with a non-zero electronic spin are extremely sensitive to perturbations due to magnetic field fluctuations, normally present in the environment and in the host crystal. In other materials with similar sensitivity to magnetic fields, this problem is typically suppressed by techniques involving huge external magnetic fields (around some Teslas), which are impossible to achieve without additional expensive equipment such as superconducting magnets. However, the internal states of ytterbium in our crystal were found to have a nice “stability valley” for magnetic field values close to zero. Its sensitivity to fluctuations is dependent on the value of the magnetic fields, and it happens to be null when no field is present at all!

The spin property of ytterbium’s electrons offers another useful feature. Despite the insensitivity to the slow field fluctuations due to the environment, the quantum information stored within the electrons can efficiently be manipulated using microwave pulses. This opens the possibility that a future quantum memory based on ytterbium could interact directly with superconducting qubits, which are at the core of the most commercially exploited quantum computing platforms. These qubits are typically controlled with signals in a similar range of frequencies and cannot be exposed to the high magnetic fields required by other rare earths.

Our results were published in two papers, one highlighting the applicative potential of ytterbium in Nature Materials and one reporting the underlying spectroscopic properties of the material in Physical Review. We also had the chance to present the work at several conferences, and to a broader public thanks to scientific news outlets around the web (for instance, see Science Daily).

Our workhorse: europium

While the ytterbium project progressed towards the implementation of the first storage experiments, I switched to another rare earth element being studied for a longer time in our labs: europium. Its main strength is the long coherence lifetime, which made it one of the main contenders for implementing a quantum repeater, together with praseodymium. In europium, a group in Australia obtained the record coherence time (original paper here) extrapolated from measured data: 6 hours, achieved with a sophisticated method of suppression of magnetic noise at an applied 7 Teslas of magnetic field. We do not need to reach those values for practical repeaters, but it shows the potential of europium.

A europium-doped YSO crystal, of about 1 cm in length, as visibile from a window of our cryostat, while our yellow laser shines through it. The coil enveloping the crystal is used to address the spin states of europium via an oscillating magnetic field.

In our group, europium in a YSO host was shown (original paper here) to be able to create pairs of single photons correlated in time, with a time delay between them. More precisely, after being excited by a weak laser pulse, an ion of europium can change its spin state by emitting a single photon. This photon heralds a successful excitation of a single spin of the ensemble. After some time, which amounted to 1 ms in our last implementation, this excitation is released as a second photon. Using certain test, one can prove that the second photon really originated from the same excitation that produced the first one. The experiment outlined forms the basis of the DLCZ quantum repater (named after its inventors, Duan, Lukin, Cirac and Zoller), which we adapted to our crystals, and that can be used to entangle two distant nodes in a quantum network. Based on these results, we have implemented several improvements of the setup used to control our quantum memory, focused on the reduction of the noise that limited the previous experiment.

Right now, we find ourselves at the point where all these improvements are being combined and tested, in order to show that pairs of entangled photons can be produced in europium, and afterwards converted into telecom frequencies. In the meantime, ytterbium is still progressing and being used in our first storage protocols. As mentioned before, all materials have their own strengths and weaknesses, making them suitable for different applications depending on which features we want our repeater to have. In any case, we will continue working towards the goal of preparing a functional quantum repeater unit and implementing it in a fibre network.

QCALL

Quantum Communications for ALL